题目内容
已知函数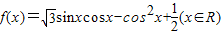
(I)求函数f(x)的最小正周期及在区间
 上的值域;
上的值域;(Ⅱ)在△ABC中,角A、B、C所对的边分别是a、b、c,又
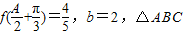 的面积等于3,求边长a的值.
的面积等于3,求边长a的值.
【答案】分析:(Ⅰ)直接利用二倍角公式以及两角差的正弦函数化简函数的表达式,求出函数的周期,根据x的范围求出2x- 的范围,集合正弦函数的值域求出所求函数的值域.
的范围,集合正弦函数的值域求出所求函数的值域.
(Ⅱ)根据题目的条件,求出cosA,sinA以及c的值,通过余弦定理求解即可得到a的值.
解答:解:(Ⅰ)因为函数 =sin(2x-
=sin(2x- ),
),
故f(x)的最小正周期为π,x∈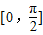 时,2x-
时,2x-
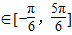 ,
,
所求函数的值域为 .
.
(Ⅱ)∵ ,∴cosA=
,∴cosA= ,∴sinA=
,∴sinA= ,
,
∵S= ,b=2,sinA=
,b=2,sinA= ,
,
∴c× ,∴c=5
,∴c=5
由余弦定理a2=b2+c2-2bccosA=4+25-2× =13,
=13,
∴a= .
.
点评:本题考查两角和与差的三角函数,二倍角公式的应用,余弦定理的应用,考查计算能力.
 的范围,集合正弦函数的值域求出所求函数的值域.
的范围,集合正弦函数的值域求出所求函数的值域.(Ⅱ)根据题目的条件,求出cosA,sinA以及c的值,通过余弦定理求解即可得到a的值.
解答:解:(Ⅰ)因为函数
 =sin(2x-
=sin(2x- ),
),故f(x)的最小正周期为π,x∈
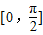 时,2x-
时,2x-
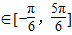 ,
,所求函数的值域为
 .
.(Ⅱ)∵
 ,∴cosA=
,∴cosA= ,∴sinA=
,∴sinA= ,
,∵S=
 ,b=2,sinA=
,b=2,sinA= ,
,∴c×
 ,∴c=5
,∴c=5由余弦定理a2=b2+c2-2bccosA=4+25-2×
 =13,
=13,∴a=
 .
.点评:本题考查两角和与差的三角函数,二倍角公式的应用,余弦定理的应用,考查计算能力.

练习册系列答案
相关题目

 的单调区间与极值;
的单调区间与极值;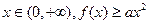 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
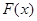 的最小值;
的最小值;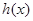 和
和 定义域内的任意实数
定义域内的任意实数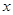 ,若存在常数
,若存在常数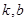 ,使得不等式
,使得不等式 和
和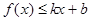 都成立,则称直线
都成立,则称直线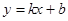 是函数
是函数 ,
,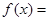
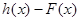 ,试问函数
,试问函数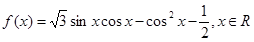
 的最小值和最小正周期;
的最小值和最小正周期;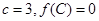 ,若向量
,若向量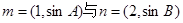 共线,求a,b的值。
共线,求a,b的值。