题目内容
设 均为正数,且
均为正数,且 ,则
,则 的最小值为 .
的最小值为 .
 均为正数,且
均为正数,且 ,则
,则 的最小值为 .
的最小值为 . 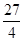
试题分析:根据题意,由于
 均为正数,且
均为正数,且 ,则可知
,则可知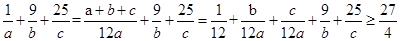 ,那么利用均值不等式可知,
,那么利用均值不等式可知, 的最小值为
的最小值为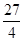 ,故答案为
,故答案为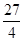 。
。点评:主要是考查了均值不等式的求解最值的运用,属于基础题。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
题目内容
 均为正数,且
均为正数,且 ,则
,则 的最小值为 .
的最小值为 . 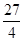
 均为正数,且
均为正数,且 ,则可知
,则可知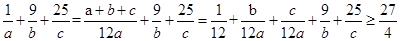 ,那么利用均值不等式可知,
,那么利用均值不等式可知, 的最小值为
的最小值为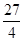 ,故答案为
,故答案为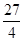 。
。
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案