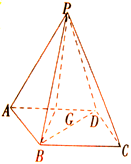
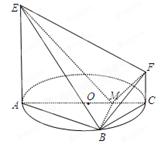
题目内容
如图,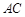 是圆
是圆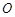 的直径,点
的直径,点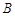 在圆
在圆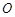 上,
上,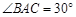 ,
,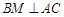 交
交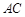 于点
于点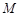 ,
,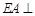 平面
平面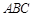 ,
,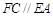 ,
, .
.
(1)证明: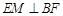 ;
;
(2)求平面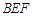 与平面
与平面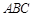 所成的锐二面角的大小.
所成的锐二面角的大小.
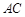 是圆
是圆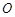 的直径,点
的直径,点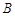 在圆
在圆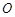 上,
上,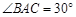 ,
,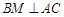 交
交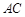 于点
于点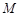 ,
,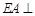 平面
平面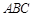 ,
,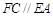 ,
, .
.
(1)证明:
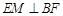 ;
;(2)求平面
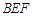 与平面
与平面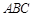 所成的锐二面角的大小.
所成的锐二面角的大小.(1)见解析 (2)二面角的余弦值为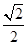
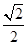
(I)本小题通过证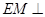 平面MBF即可.
平面MBF即可.
(2)本小题的关键是作出二面角的平面角.延长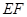 交
交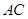 于
于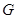 ,连
,连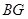 ,过
,过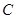 作
作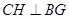 ,连结
,连结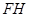 .证
.证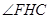 为平面
为平面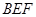 与平面
与平面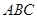 所成的二面角的平面角即可
所成的二面角的平面角即可
(法一)(1)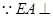 平面
平面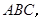
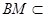 平面
平面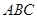 ,
, 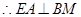 .………1分
.………1分
又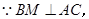
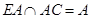 ,
,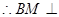 平面
平面 而
而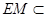 平面
平面
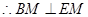 . ……3分
. ……3分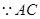 是圆
是圆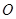 的直径,
的直径,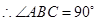 .
.
又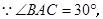
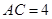 ,
,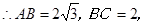
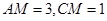 .
.
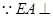 平面
平面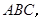
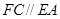 ,
,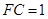 ,
, 平面
平面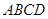 .
.
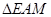 与
与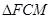 都是等腰直角三角形.
都是等腰直角三角形.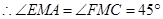 .
.
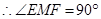 ,即
,即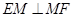 (也可由勾股定理证得).
(也可由勾股定理证得).
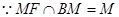 ,
, 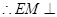 平面
平面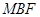 .而
.而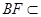 平面
平面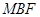 ,
,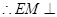
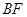 . 7分
. 7分
(2)延长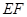 交
交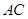 于
于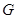 ,连
,连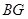 ,过
,过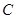 作
作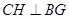 ,连结
,连结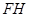 .
.
由(1)知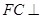 平面
平面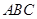 ,
,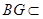 平面
平面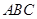 ,
,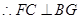 .而
.而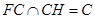 ,
,
 平面
平面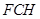 .
.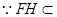 平面
平面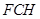 ,
,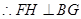 ,
,
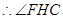 为平面
为平面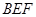 与平面
与平面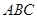 所成的二面角的平面角.
所成的二面角的平面角.
在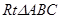 中,
中,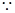
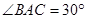 ,
,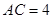 ,
,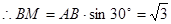 .
.
由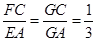 ,得
,得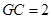 .
.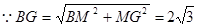 .2
.2
又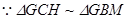 ,
,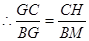 ,则
,则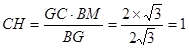 .
.
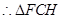 是等腰直角三角形,
是等腰直角三角形,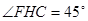 .
.
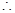 平面
平面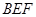 与平面
与平面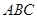 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为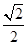 .…14分
.…14分
(法二)(1)同法一,得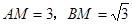 .
.
如图,以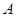 为坐标原点,垂直于
为坐标原点,垂直于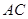 、
、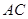 、
、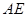 所在直线为
所在直线为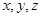 轴建立空间直角坐标系.
轴建立空间直角坐标系.
由已知条件得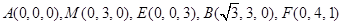 ,
,
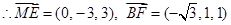 .由
.由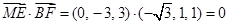 ,
,
得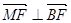 ,
, 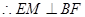 . …7分
. …7分
(2)由(1)知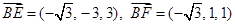 .设平面
.设平面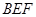 的法向量为
的法向量为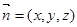 ,
,
由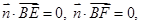 得
得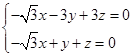 ,
,
令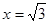 得
得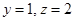 ,
,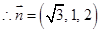 , ……9分由已知
, ……9分由已知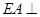 平面
平面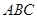 ,所以取面
,所以取面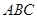 的法向量为
的法向量为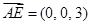 ,设平面
,设平面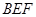 与平面
与平面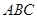 所成的锐二面角为
所成的锐二面角为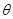 ,
,
则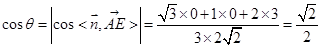 ,
, 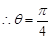
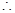 平面
平面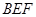 与平面
与平面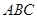 所成的锐二面角为
所成的锐二面角为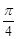
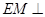 平面MBF即可.
平面MBF即可.(2)本小题的关键是作出二面角的平面角.延长
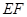 交
交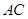 于
于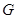 ,连
,连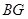 ,过
,过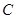 作
作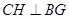 ,连结
,连结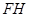 .证
.证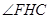 为平面
为平面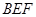 与平面
与平面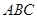 所成的二面角的平面角即可
所成的二面角的平面角即可(法一)(1)
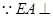 平面
平面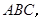
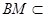 平面
平面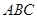 ,
, 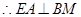 .………1分
.………1分又
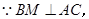
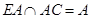 ,
,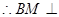 平面
平面 而
而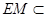 平面
平面
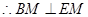 . ……3分
. ……3分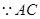 是圆
是圆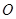 的直径,
的直径,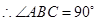 .
.又
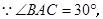
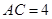 ,
,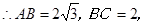
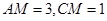 .
.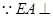 平面
平面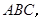
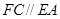 ,
,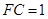 ,
, 平面
平面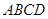 .
.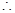
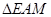 与
与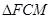 都是等腰直角三角形.
都是等腰直角三角形.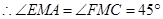 .
.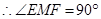 ,即
,即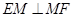 (也可由勾股定理证得).
(也可由勾股定理证得).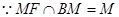 ,
, 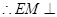 平面
平面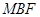 .而
.而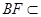 平面
平面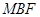 ,
,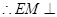
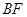 . 7分
. 7分(2)延长
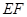 交
交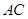 于
于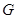 ,连
,连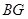 ,过
,过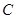 作
作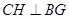 ,连结
,连结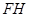 .
.由(1)知
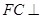 平面
平面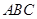 ,
,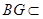 平面
平面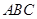 ,
,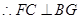 .而
.而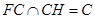 ,
, 平面
平面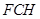 .
.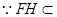 平面
平面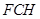 ,
,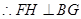 ,
,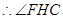 为平面
为平面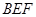 与平面
与平面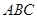 所成的二面角的平面角.
所成的二面角的平面角.在
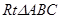 中,
中,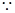
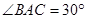 ,
,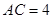 ,
,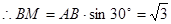 .
.由
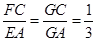 ,得
,得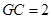 .
.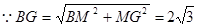 .2
.2 又
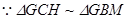 ,
,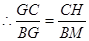 ,则
,则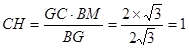 .
. 是等腰直角三角形,
是等腰直角三角形,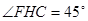 .
. 平面
平面 与平面
与平面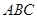 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为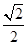 .…14分
.…14分(法二)(1)同法一,得
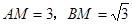 .
.如图,以
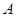 为坐标原点,垂直于
为坐标原点,垂直于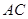 、
、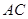 、
、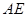 所在直线为
所在直线为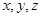 轴建立空间直角坐标系.
轴建立空间直角坐标系.由已知条件得
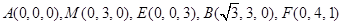 ,
,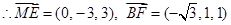 .由
.由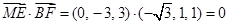 ,
,得
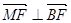 ,
, 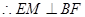 . …7分
. …7分(2)由(1)知
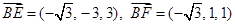 .设平面
.设平面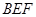 的法向量为
的法向量为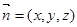 ,
,由
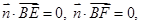 得
得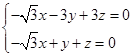 ,
,令
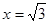 得
得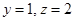 ,
,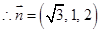 , ……9分由已知
, ……9分由已知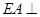 平面
平面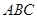 ,所以取面
,所以取面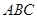 的法向量为
的法向量为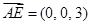 ,设平面
,设平面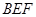 与平面
与平面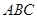 所成的锐二面角为
所成的锐二面角为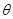 ,
,则
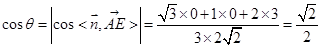 ,
, 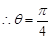
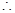 平面
平面 与平面
与平面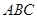 所成的锐二面角为
所成的锐二面角为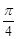

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 中,
中,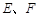 分别为
分别为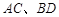 的中点,若
的中点,若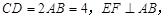 则
则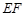 与
与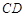 所成的角为
所成的角为







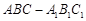 中已知
中已知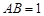 ,
, 在棱
在棱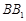 上,且
上,且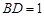 ,若
,若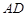 与平面
与平面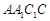 所成的角为
所成的角为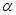 ,则
,则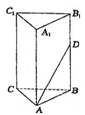




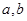 所成的角为
所成的角为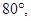 过空间一点O与
过空间一点O与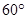 的直线有___________条
的直线有___________条 中,
中,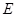 为
为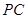 的中点,则
的中点,则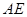 与平面
与平面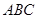 所成的角的正弦值为( )
所成的角的正弦值为( )



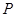 是正四面体
是正四面体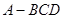 的棱
的棱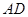 中点,则直线
中点,则直线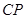 与平面
与平面 所成角的正弦值为__________.
所成角的正弦值为__________.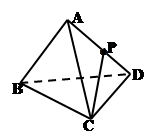
 中,
中, 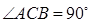 ,
,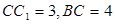 ,
, 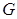 是
是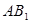 和
和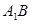 的交点, 若
的交点, 若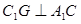 .
. 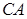 的长; (2)求点
的长; (2)求点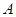 到平面
到平面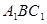 的距离;
的距离;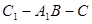 的平面角的正弦值的大小.
的平面角的正弦值的大小.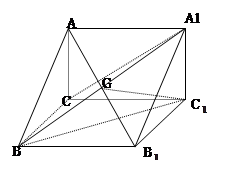
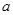 的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,
的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,