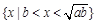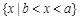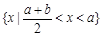题目内容
对于函数y=f(x)(x∈I),y=g(x)(x∈I),若对任意x∈I,存在x0使得f(x)≥f(x0),g(x)≥g(x0)且f(x0)=g(x0),则称f(x),g(x)为“兄弟函数”,已知f(x)=x2+px+q,g(x)=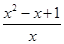 是定义在区间
是定义在区间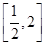 上的“兄弟函数”,那么函数f(x)在区间
上的“兄弟函数”,那么函数f(x)在区间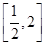 上的最大值为( )
上的最大值为( )
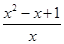 是定义在区间
是定义在区间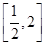 上的“兄弟函数”,那么函数f(x)在区间
上的“兄弟函数”,那么函数f(x)在区间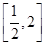 上的最大值为( )
上的最大值为( )A. | B.2 | C.4 | D. |
B
g(x)=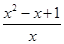 =x+
=x+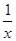 -1≥2-1=1,
-1≥2-1=1,
当且仅当x=1时,等号成立,
∴f(x)在x=1处有最小值1,
即p=-2,
12-2×1+q=1,q=2,
∴f(x)=x2-2x+2=(x-1)2+1,
∴f(x)max=f(2)=(2-1)2+1=2.
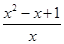 =x+
=x+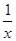 -1≥2-1=1,
-1≥2-1=1,当且仅当x=1时,等号成立,
∴f(x)在x=1处有最小值1,
即p=-2,
12-2×1+q=1,q=2,
∴f(x)=x2-2x+2=(x-1)2+1,
∴f(x)max=f(2)=(2-1)2+1=2.

练习册系列答案
相关题目

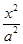 -
-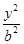 =1(a>0,b>0)的离心率为2,则
=1(a>0,b>0)的离心率为2,则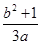 的最小值为( )
的最小值为( )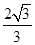
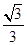
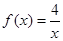 的图像交于P、Q两点,则线段PQ长的最小值是____
的图像交于P、Q两点,则线段PQ长的最小值是____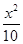 -30x+4 000,则每吨的成本最低时的年产量为________.
-30x+4 000,则每吨的成本最低时的年产量为________.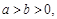 集合
集合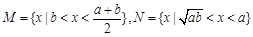 ,则集合
,则集合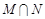 等于( )
等于( )