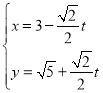题目内容
【题目】设A,B为曲线C:![]() 上两点,A与B的横坐标之和为4.
上两点,A与B的横坐标之和为4.
(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM⊥BM,求直线AB的方程.
【答案】(1)1;(2)y=x+7..
【解析】
(1)设![]() 两点坐标,代入抛物线方程 相减后可求得
两点坐标,代入抛物线方程 相减后可求得![]() 的斜率;
的斜率;
(2)由C在M处的切线与直线AB平行,可求得切点![]() 坐标,设直线AB的方程为y=x+m,代入抛物线方程可得
坐标,设直线AB的方程为y=x+m,代入抛物线方程可得![]() 中点为
中点为![]() ,AM⊥BM等价于
,AM⊥BM等价于![]() ,这样可求得
,这样可求得![]() 值.
值.
解:(1)设A(x1,y1),B(x2,y2),则x1≠x2,![]() ,x1+x2=4,于是直线AB的斜率
,x1+x2=4,于是直线AB的斜率![]() .
.
(2)由![]() ,得
,得![]() .
.
设M(x3,y3),由题设知![]() ,解得x3=2,于是M(2,1).
,解得x3=2,于是M(2,1).
设直线AB的方程为y=x+m,故线段AB的中点为N(2,2+m),|MN|=|m+1|.
将y=x+m代入![]() 得x2-4x-4m=0.
得x2-4x-4m=0.
当Δ=16(m+1)>0,即m>-1时,![]() .
.
从而![]() .
.
由题设知|AB|=2|MN|,即![]() ,解得m=7.
,解得m=7.
所以直线AB的方程为y=x+7.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目