题目内容
【题目】已知函数f（x）满足f（x）+f（2﹣x）=2，当x∈（0，1]时，f（x）=x2 ， 当x∈（﹣1，0]时， 
，若定义在（﹣1，3）上的函数g（x）=f（x）﹣t（x+1）有三个不同的零点，则实数t的取值范围是（ ）
A.
B.
C.
D.
【答案】D
【解析】解：由题可知函数在x∈（﹣1，1]上的解析式为 
，
又由f（x）+f（2﹣x）=2可知f（x）的图象关于（1，1）点对称，
可将函数f（x）在x∈（﹣1，3）上的大致图象呈现如图：
根据y=t（x+1）的几何意义，x轴位置和图中直线位置为y=t（x+1）表示直线的临界位置，其中x∈[1，2）时，
f（x）=﹣（x﹣2）2+2，联立 
，并令△=0，可求得 
．
因此直线的斜率t的取值范围是 
．
故选：D．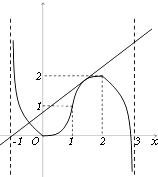
练习册系列答案
相关题目
