题目内容
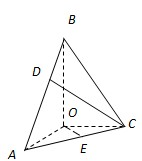（2009•金山区二模）如图，在三棱锥B-ACO中，BO、AO、CO所在直线两两垂直，且AO=CO，∠BAO=60°，E是AC的中点，三棱锥B-ACO的体积为
| ||
| 6 |
（1）求三棱锥B-ACO的高；
（2）在线段AB上取一点D，当D在什么位置时，
| DC |
| OE |
| 1 |
| 4 |
分析：（1）由题意的BO⊥平面ACO，即BO就是三棱锥B-ACO的高，然后根据体积建立等式关系，解之即可求出所求；
（2）以O为原点，OA为x轴，OC为y轴，OB为z轴，建立空间直角坐标系，设D（x，0，
（1-x）），设
和
的夹角为θ，则coaθ=
=
建立等式关系，解之即可求出x的值，从而可判定点D的位置．
（2）以O为原点，OA为x轴，OC为y轴，OB为z轴，建立空间直角坐标系，设D（x，0，
| 3 |
| DC |
| OE |
| ||||
/
|
| 1 |
| 4 |
解答：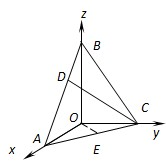
解：（1）由题意的BO⊥平面ACO，即BO就是三棱锥B-ACO的高，…（2分）
在Rt△ABO中，设AO=a，∠BAO=60°，所以BO=
a，
CO=a，所以VB-ACO=
×
×AO×BO×CO=
a3=
．
所以a=1，所以三棱锥的高BO为
．…（4分）
（2）以O为原点，如图建立空间直角坐标系…（5分）
设D（x，0，
（1-x）），则C（0，1，0），E（
，
，0 ）
=（-x，1，
（ x-1）），
=（
，
，0）…（10分）
设
和
的夹角为θ
则coaθ=
=
=
…（12分）
解之得，x=2（舍去）或x=
，
所以当D在AB的中点时，
和
的夹角大小为arccos
．…（14分）
解：（1）由题意的BO⊥平面ACO，即BO就是三棱锥B-ACO的高，…（2分）在Rt△ABO中，设AO=a，∠BAO=60°，所以BO=
| 3 |
CO=a，所以VB-ACO=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 6 |
| ||
| 6 |
所以a=1，所以三棱锥的高BO为
| 3 |
（2）以O为原点，如图建立空间直角坐标系…（5分）
设D（x，0，
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| DC |
| 3 |
| OE |
| 1 |
| 2 |
| 1 |
| 2 |
设
| DC |
| OE |
则coaθ=
| ||||
/
|
=
| ||||||
|
| 1 |
| 4 |
解之得，x=2（舍去）或x=
| 1 |
| 2 |
所以当D在AB的中点时，
| DC |
| OE |
| 1 |
| 4 |
点评：本题主要考查了锥体的体积，以及利用空间向量解决空间两异面直线所成角，同时考查了空间想象能力，推理论证的能力，属于中档题．
练习册系列答案
相关题目