题目内容
设函数f(x)=3sinx+2cosx+1。若实数a、b、c使得af(x)+bf(x?c)=1对任意实数x恒成立,则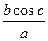 的值等于( )
的值等于( )
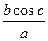 的值等于( )
的值等于( )A.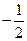 | B.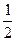 | C.?1 | D.1 |
C
令c=π,则对任意的x∈R,都有f(x)+f(x?c)=2,于是取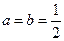 ,c=π,则对任意的x∈R,af(x)+bf(x?c)=1,由此得
,c=π,则对任意的x∈R,af(x)+bf(x?c)=1,由此得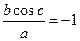 。
。
一般地,由题设可得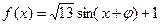 ,
,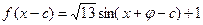 ,其中
,其中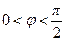 且
且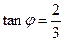 ,于是af(x)+bf(x?c)=1可化为
,于是af(x)+bf(x?c)=1可化为
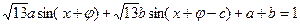 ,即
,即
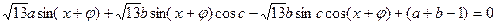 ,所以
,所以
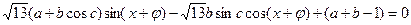 。
。




由已知条件,上式对任意x∈R恒成立,故必有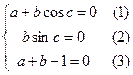 ,
,
若b=0,则由(1)知a=0,显然不满足(3)式,故b≠0。所以,由(2)知sinc=0,故c=2kπ+π或c=2kπ(k∈Z)。当c=2kπ时,cosc=1,则(1)、(3)两式矛盾。故c=2kπ+π(k∈Z),cosc=?1。由(1)、(3)知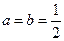 ,所以
,所以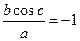 。
。
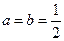 ,c=π,则对任意的x∈R,af(x)+bf(x?c)=1,由此得
,c=π,则对任意的x∈R,af(x)+bf(x?c)=1,由此得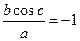 。
。一般地,由题设可得
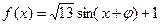 ,
,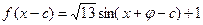 ,其中
,其中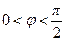 且
且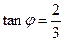 ,于是af(x)+bf(x?c)=1可化为
,于是af(x)+bf(x?c)=1可化为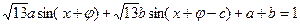 ,即
,即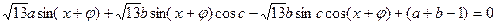 ,所以
,所以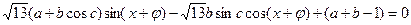 。
。




由已知条件,上式对任意x∈R恒成立,故必有
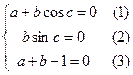 ,
,若b=0,则由(1)知a=0,显然不满足(3)式,故b≠0。所以,由(2)知sinc=0,故c=2kπ+π或c=2kπ(k∈Z)。当c=2kπ时,cosc=1,则(1)、(3)两式矛盾。故c=2kπ+π(k∈Z),cosc=?1。由(1)、(3)知
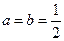 ,所以
,所以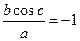 。
。
练习册系列答案
相关题目
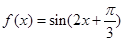 向右平移
向右平移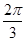 个单位,再将所得的函数图象上的各点纵坐标不 变,横坐标变为原来的2倍,得到函数
个单位,再将所得的函数图象上的各点纵坐标不 变,横坐标变为原来的2倍,得到函数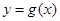 的图象,则函数
的图象,则函数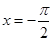 ,
,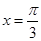 ,
,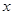 轴围成的图形面积为
轴围成的图形面积为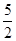
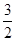
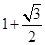
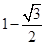
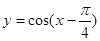 的图像向左平移
的图像向左平移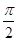 个单位后得到的图像的函数解析式为
个单位后得到的图像的函数解析式为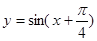
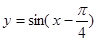
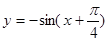
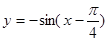
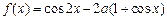 的最小值为
的最小值为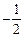 ,则
,则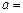 .
.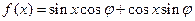 (其中
(其中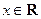 ,
,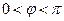 ).
).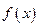 的最小正周期;(2)若函数
的最小正周期;(2)若函数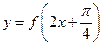 的图像关于直线
的图像关于直线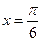 对称,求
对称,求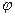 的值.
的值.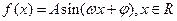 (其中
(其中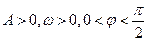 )的周期为
)的周期为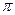 ,且图象上一个最低点为
,且图象上一个最低点为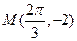 。
。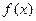 的解析式;
的解析式;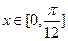 ,求
,求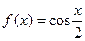 ,下面四个等式
,下面四个等式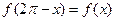 ②
②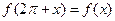 ③
③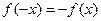 ④
④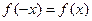
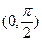 上为增函数且以
上为增函数且以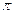 为周期的函数是( ).
为周期的函数是( ).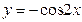
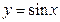
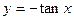
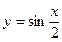
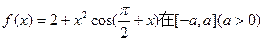 上的最大值与最小值分别为M、m,则M+m的值为 ( )
上的最大值与最小值分别为M、m,则M+m的值为 ( )