题目内容
从编号为1、2、3、4的四个不同小球中取出三个不同的小球放入编号为1、2、3的三个不同盒子里,每个盒子放一个球,则1号球不放1号盒子,3号球不放3号盒子的放法共有 种(以数字作答).
14
解:由题意知元素的限制条件比较多,要分类解决,
当选出的三个球是1、2、3或1、3、4时,以前一组为例,
1号球在2号盒子里,2号和3号只有一种方法,
1号球在3号盒子里,2号和3号各有两种结果,
选1、2、3时共有3种结果,
选1、3、4时也有3种结果,
当选到1、2、4或2、3、4时,各有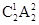 =4种结果,
=4种结果,
由分类和分步计数原理得到共有3+3+4+4=14种结果,
当选出的三个球是1、2、3或1、3、4时,以前一组为例,
1号球在2号盒子里,2号和3号只有一种方法,
1号球在3号盒子里,2号和3号各有两种结果,
选1、2、3时共有3种结果,
选1、3、4时也有3种结果,
当选到1、2、4或2、3、4时,各有
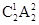 =4种结果,
=4种结果,由分类和分步计数原理得到共有3+3+4+4=14种结果,

练习册系列答案
相关题目
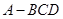 的每条棱染色,要求每条棱只染一种颜色且共顶点的棱染不同的颜色,则不同的染色方法共有( )种。
的每条棱染色,要求每条棱只染一种颜色且共顶点的棱染不同的颜色,则不同的染色方法共有( )种。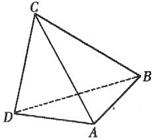
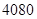
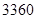
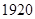
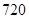
 1 B.6 C.9 D.27
1 B.6 C.9 D.27