题目内容
设随机变量X服从正态分布N（0，1），已知P（X＜-2）=0.025，则P（|X|＜2）=______．
解法一：∵X～N（0，1）
∴P（|X|＜2）
=P（-2＜X＜2）
=Φ（2）-Φ（-2）
=1-2Φ（-2）
=0.950
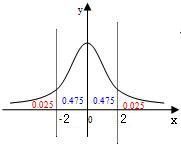
解法二：因为曲线的对称轴是直线x=0，
所以由图知P（X＞2）=P（X≤-2）=Φ（-2）=0.025
∴P（|X|＜2）=1-0.25-0.25=0.950
故答案为：0.950．
∴P（|X|＜2）
=P（-2＜X＜2）
=Φ（2）-Φ（-2）
=1-2Φ（-2）
=0.950
解法二：因为曲线的对称轴是直线x=0，
所以由图知P（X＞2）=P（X≤-2）=Φ（-2）=0.025
∴P（|X|＜2）=1-0.25-0.25=0.950
故答案为：0.950．
练习册系列答案
相关题目
，统计结果显示学生考试成绩在80分到100分之间的人数约占总人数的
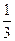，则此次考试成绩不低于120分的学生约有 人．
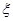服从正态分布
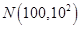，已知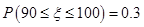
，估计该班数学成绩在110以上的学生人数为 ．