题目内容
8.已知等差数列{an}的前n项和为Sn,且a2+a6=14,S5=25.(1)求an及Sn;
(2)数列{bn}中,令b1=1,bn=$\frac{4}{{{a}_{n}}^{2}-1}$ (n≥2,n∈N*),证明:数列{bn}的前n项和Tn<2.
分析 (1)设等差数列{an}的公差为d,由a2+a6=14,S5=25.利用等差数列的通项公式及其前n项和公式即可得出.
(2)bn=$\frac{4}{(2n-1)^{2}-1}$=$\frac{1}{n-1}-\frac{1}{n}$,(n≥2,n∈N*),利用“裂项求和”即可得出.
解答 (1)解:设等差数列{an}的公差为d,∵a2+a6=14,S5=25.
∴$\left\{\begin{array}{l}{2{a}_{1}+6d=14}\\{5{a}_{1}+\frac{5×4}{2}d=25}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=2}\end{array}\right.$,
∴an=2n-1,
Sn=$\frac{n(1+2n-1)}{2}$=n2.
(2)证明:∵bn=$\frac{4}{{{a}_{n}}^{2}-1}$=$\frac{4}{(2n-1)^{2}-1}$=$\frac{1}{n(n-1)}$=$\frac{1}{n-1}-\frac{1}{n}$,(n≥2,n∈N*),
∴Tn=1+$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n-1}-\frac{1}{n})]$
=1+1-$\frac{1}{n}$<2.
点评 本题考查了等差数列的通项公式及其前n项和公式、“裂项求和”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
18.等比数列{an}的前n 项和为S n,若an>0,q>1,a3+a5=20,a2a6=64则公比q为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
19.若α是锐角,且cos(α+$\frac{π}{3}$)=$\frac{\sqrt{3}}{3}$,则sinα的值等于( )
| A. | $\frac{\sqrt{6}+3}{6}$ | B. | $\frac{\sqrt{6}-3}{6}$ | C. | $\frac{2\sqrt{6}+1}{6}$ | D. | $\frac{2\sqrt{6}-1}{6}$ |
3.不等式组$\left\{\begin{array}{l}{{x}^{2}-1<0}\\{{x}^{2}-3x>0}\end{array}\right.$的解集是( )
| A. | {x|-1<x<1} | B. | {x|-1<x<0} | C. | {x|0<x<1} | D. | {x|0<x<3} |
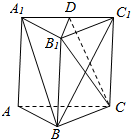 如图所示,棱柱ABC-A1B1C1的侧面BCC1B1是菱形,设D是A1C1上的点且A1B∥平面B1CD,则A1D:DC1的值为1.
如图所示,棱柱ABC-A1B1C1的侧面BCC1B1是菱形,设D是A1C1上的点且A1B∥平面B1CD,则A1D:DC1的值为1.