题目内容
新学期开始,学校接受6名师大学生生到校实习,学校要把他们分配到三个年级,每个年级2人,其中甲必须在高一年级,乙和丙均不能在高三年级,则不同的安排种数为
| A.18 | B.15 | C.12 | D.9 |
D
解析试题分析:当乙丙都在高二时,余下的三人中选一人在高一,其余二人在高三,共有3种安排方法;当乙丙一个在高一,一个在高二时,先选择一人在高一,2种选法,余下的三人选其一在高二共有3种选法,所以有6种安排方法。两种方案共有9种安排种数
考点:排列组合问题
点评:本题中甲乙丙三元素较特殊,应优先安排

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
从4名男生 和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,
则不同的选法共有 ( )
| A.140种 | B.120种 | C.35种 | D.34种 |
我们把各位数字之和为6的四位数称为“六合数”(如2013是“六合数”),则“六合数”中首位为2的“六合数”共有
| A.18个 | B.15个 | C.12个 | D.9个 |
下列排列数中,等于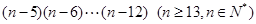 的是( )
的是( )
A.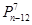 | B.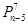 | C.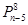 | D.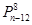 |
从10名大学毕业生中选3人担任村长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数为
| A.85 | B.56 | C.49 | D.28 |
若(x+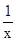 )n展开式的二项式系数之和为64,则展开式的常数项为( )
)n展开式的二项式系数之和为64,则展开式的常数项为( )
| A.10 | B.20 | C.30 | D.120 |
已知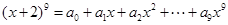 ,则
,则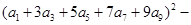
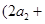
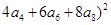 的值为( )
的值为( )
A.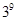 | B.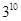 | C.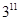 | D.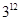 |
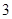 张不同的电影票全部分给
张不同的电影票全部分给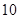 个人,每人至多一张,则有不同分法的种数是( )
个人,每人至多一张,则有不同分法的种数是( )
 位数的十位数字比个位数字和百位数字都大,则称这个数为“伞数”,现从1、2、3
位数的十位数字比个位数字和百位数字都大,则称这个数为“伞数”,现从1、2、3 、4、5、6这六个数字中任取3个,组成无重复数字的三位数,其中“伞数”的个数为
、4、5、6这六个数字中任取3个,组成无重复数字的三位数,其中“伞数”的个数为