题目内容
20．
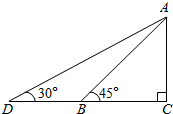如图，有一条长为50$\sqrt{2}$（米）的斜坡AB，它的坡角为45°，现保持坡高AC不变，将坡角改为30°，则斜坡AD的长为100（米）．
分析 分别解三角形ABC和△ACD即可．
解答 解：在△ABC中，AB=50$\sqrt{2}$，∠ACB=90°，∠ABC=45°，所以AC=$\frac{\sqrt{2}}{2}$AB=50米，
在△ADC中，∠ADC=30°，∠ACD=90°，AC=50，
所以AD=$\frac{AC}{sin∠ADC}$=$\frac{50}{\frac{1}{2}}$=100；
故答案为：100．
点评 本题考查了解三角形在实际中的应用；关键是将问题放到三角形中，求边长．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．根据秦九韶算法求x=-1时f（x）=4x4+3x3-6x2+x-1的值，则v2为（ ）
| A． | -1 | B． | -5 | C． | 21 | D． | -22 |
11．定义在上（0，$\frac{π}{4}$）的函数f（x）满足2f（x）＜f′（x）tan2x，f′（x）是f（x）的导函数，则（ ）
| A． | $\sqrt{3}$f（$\frac{π}{12}$）＜f（$\frac{π}{6}$） | B． | f（$\frac{1}{4}$）$＞2f（\frac{π}{12}）$sin$\frac{1}{2}$ | C． | $\sqrt{3}$f（$\frac{π}{8}$）＞$\sqrt{2}$f（$\frac{π}{6}$） | D． | $\sqrt{2}$f（$\frac{π}{12}$）＞f（$\frac{π}{8}$） |
8．已知角α的终边与圆x2+y2=4相交于点P（1，-$\sqrt{3}$），则sinα的值为（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
15．直线x+1=0的倾斜角为（ ）
| A． | 0 | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | $\frac{3π}{4}$ |
5．直线x-y=0的倾斜角大小为（ ）
| A． | 0° | B． | 45° | C． | 60° | D． | 90° |
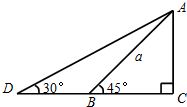如图，有一条长为a米的斜坡AB，它的坡角为45°，现保持坡高AC不变，将坡角改为30°，则斜坡AD的长为$\sqrt{2}$a米．