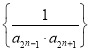题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 上的最小值;
上的最小值;
(2)若直线![]() 是函数
是函数![]() 的切线方程,求实数
的切线方程,求实数![]() 的值;
的值;
(3)若![]() ,证明:对任意实数
,证明:对任意实数![]() ,
,![]() 恒成立.
恒成立.
【答案】(1)0(2)![]() (3)见解析
(3)见解析
【解析】
(1)求出函数![]() 的到函数
的到函数![]() ,可得
,可得![]() 的单调性,从而得出其最小值.
的单调性,从而得出其最小值.
(2) 设切点为![]() ,由直线
,由直线![]() 是函数
是函数![]() 的切线方程,则
的切线方程,则![]() ,即
,即 ,又
,又![]() ,即
,即![]() ,即得
,即得![]() ,即求出函数
,即求出函数![]() 的零点即可.
的零点即可.
(3) 因为![]() ,所以当
,所以当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() ,设
,设![]() ,可得
,可得![]() 恒成立,且
恒成立,且![]() ,则
,则![]() 时,
时,![]() ,即
,即![]() ,即
,即![]() ,同理可得
,同理可得![]() ,从而可证.
,从而可证.
解:(1)由于![]() ,则
,则![]() ,从而
,从而![]() 在
在![]() 单调递增,从而
单调递增,从而![]() .
.
(2)![]() ,由题可知,设切点为
,由题可知,设切点为![]() ,
,
则由![]() ,整理得
,整理得![]() .
.
当![]() 时,不可能;当
时,不可能;当![]() 时,得
时,得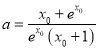 ①.
①.
又![]() ,即
,即![]() ②.
②.
由①②可得,![]() .
.
令![]() ,则
,则![]() ,注意到
,注意到![]() .
.
令![]() ,则
,则![]() ,注意到
,注意到![]() .
.
令![]() ,则
,则![]() 恒成立.
恒成立.
可得![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,所以
,所以![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递增,可知
上单调递增,可知![]() 是方程的唯一解.
是方程的唯一解.
所以切点为![]() ,
,![]() .
.
(3)因为![]() ,
,
所以当![]() 时,
时,![]() ③,
③,
所以当![]() 时,
时,![]() ④,
④,
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,所以
,所以![]() 恒成立,且
恒成立,且![]() .
.
设![]() ,则
,则![]() .
.
此时![]() ,即
,即![]() ,结合③,得
,结合③,得![]() ,
,
即![]() ,得到
,得到![]() ,
,![]() 成立
成立
![]() ,即
,即![]() ,结合④,得
,结合④,得![]() ,
,
即![]() ,得到
,得到![]() ,
,
所以![]() ,
,![]() 成立,
成立,
所以![]() 成立,得证.
成立,得证.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
【题目】一个袋子中有红、黄、蓝、绿四个小球,有放回地从中任取一个小球,将“三次抽取后,红色小球,黄色小球都取到”记为事件M,用随机模拟的方法估计事件M发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表红、黄、蓝、绿四个小球,以每三个随机数为一组,表示取小球三次的结果,经随机模拟产生了以下18组随机数:
110 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件M发生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()