题目内容
正四面体的侧面与底面所成的二面角的余弦值为（ ）A．
B．
C．
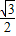
D．
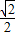
【答案】分析：由已知中正四面体的所有面都是等边三角形，取CD的中点E，连接AE，BE，由等腰三角形“三线合一”的性质，易得∠AEB即为侧面与底面所成二面角的平面角，解三角形ABE即可得到正四面体侧面与底面所成二面角的余弦值．
解答：解：不妨设正四面体为A-BCD，取CD的中点E，连接AE，BE，设四面体的棱长为2，则AE=BE=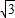
且AE⊥CD，BE⊥CD，则∠AEB即为侧面与底面所成二面角的平面角
在△ABE中，cos∠AEB=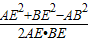
=
故正四面体侧面与底面所成二面角的余弦值是
故选A．
点评：本题考查的知识点是二面角的平面角及求法，其中确定∠AEB即为相邻两侧面所成二面角的平面角，是解答本题的关键．
解答：解：不妨设正四面体为A-BCD，取CD的中点E，连接AE，BE，设四面体的棱长为2，则AE=BE=
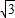
且AE⊥CD，BE⊥CD，则∠AEB即为侧面与底面所成二面角的平面角
在△ABE中，cos∠AEB=
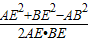=故正四面体侧面与底面所成二面角的余弦值是
故选A．
点评：本题考查的知识点是二面角的平面角及求法，其中确定∠AEB即为相邻两侧面所成二面角的平面角，是解答本题的关键．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
，AG＝
，给出下列四个命题：①AC⊥BD，②FG＝
，③侧面与底面所成二面角的余弦值为
，④
，其中真命题的序号是（ ）