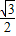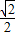题目内容
正四面体的侧面与底面所成的二面角的余弦值为（ ）
A．
| B．
| C．
| D．
|
不妨设正四面体为A-BCD，取CD的中点E，连接AE，BE，设四面体的棱长为2，则AE=BE=
且AE⊥CD，BE⊥CD，则∠AEB即为侧面与底面所成二面角的平面角
在△ABE中，cos∠AEB=
=
故正四面体侧面与底面所成二面角的余弦值是
故选A．
| 3 |
且AE⊥CD，BE⊥CD，则∠AEB即为侧面与底面所成二面角的平面角
在△ABE中，cos∠AEB=
| AE2+BE2-AB2 |
| 2AE•BE |
| 1 |
| 3 |
故正四面体侧面与底面所成二面角的余弦值是
| 1 |
| 3 |
故选A．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
，AG＝
，给出下列四个命题：①AC⊥BD，②FG＝
，③侧面与底面所成二面角的余弦值为
，④
，其中真命题的序号是（ ）
