题目内容
18.(1)设k,n∈N*,k≤n,求证:kCknkn=nCk−1n−1k−1n−1;(2)设n∈N*,n≥2,x∈R.
①求证:∑nk=0∑nk=0(k+1)Cknknxk(1-x)n-k=nx+1;
②求函数f(x)=∑nk=0∑nk=0k2Ckn2Cknxk(1-x)n-k的零点.
分析 (1)由条件利用组合数的性质以及计算公式,证得kCknkn=nCk−1n−1k−1n−1 成立.
(2)由条件利用组合数的性质化简函数的解析式,再利用函数零点的定义求出函数f(x)=∑nk=0∑nk=0k2Ckn2Cknxk(1-x)n-k的零点.
解答 (1)证明:∵kCknkn=k•n!(n−k)!k!=n!(n−k)!•(k−1)!,又nCk−1n−1=n•(n−1)!(k−1)!•(n−k)!=n!(n−k)!•(k−1)!,
∴kCkn=nCk−1n−1 成立.
(2)①∵n∈N*,n≥2,x∈R时,∑nk=0(k+1)Cknxk(1-x)n-k=∑nk=1k•Ckn•xk•(1−x)n−k+∑nk=1•Ckn•xk•(1-x)n-k,
=∑nk=1•n•Ck−1n−1•xk•(1-x)n-k+[(1-x)+x]n=nx•∑nk=1•n•Ck−1n−1•xk-1•(1-x)n-k+1=nx[(1-x)+x]n-1+1=nx+1,
∴∑nk=0(k+1)Cknxk(1-x)n-k=nx+1成立.
②函数f(x)=∑nk=0k2Cknxk(1-x)n-k=∑nk=0 k•kCkn•xk(1-x)n-k=∑nk=1 k•n•Ck−1n−1•xk(1-x)n-k
=n∑nk=1(k-1+1)•Ck−1n−1•xk(1-x)n-k =n∑nk=1(k-1)•Ck−1n−1•xk(1-x)n-k+n∑nk=1•Ck−1n−1•xk(1-x)n-k
=n∑nk=1(n-1)•Ck−2n−2•xk(1-x)n-k +nx∑nk=1•Ck−1n−1•xk-1(1-x)n-k ,
=n(n-1)x2•∑nk=2•Ck−2n−2•xk-2(1-x)n-k +nx∑nk=1•Ck−1n−1•xk(1-x)n-k =
=n(n-1)x2•[(1-x)+x]n-2+nx[(1-x)+x]n-1=n(n-1)x2+nx,
令f(x)=0,求得x=0,或x=11−n,
故函数f(x)的零点为9或11−n.
点评 本题主要考查二项式定理的应用,组合数的性质以及组合数的试算公式,属于中档题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | a、b、c三个实数中最多有一个不大于零 | |
| B. | a、b、c三个实数中最多有两个小于零 | |
| C. | a、b、c三个实数中至少有两个小于零 | |
| D. | a、b、c三个实数中至少有一个不大于零 |
| A. | →a−12→b | B. | →a+12→b | C. | -→a−12→b | D. | -→a+12→b |
| A. | ab−1 | B. | 32(b−1) | C. | 3a2(b+1) | D. | 3(a−1)2b |
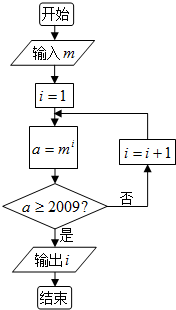 阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)
阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)