题目内容
10.已知函数f(x)=|x-2|-|x-a|(a∈R)(Ⅰ)当a=4时,求不等式f(x)<1的解集
(Ⅱ)若a<0,且不等式|f(x)|<a2恒成立,求a的取值范围.
分析 (Ⅰ)运用零点分区间的方法,去绝对值,分别解不等式,再求并集即可;
(Ⅱ)运用绝对值不等式的性质,求得|f(x)|的最大值2-a,令a2>2-a,解不等式即可得到.
解答 解:(Ⅰ)当a=4时,f(x)=|x-2|-|x-4|=$\left\{\begin{array}{l}{2,x≥4}\\{2x-6,2<x<4}\\{-2,x≤2}\end{array}\right.$,
当x≥4时,f(x)<1即2<1不成立;
当2<x<4时,f(x)<1即2x-6<1,解得x<$\frac{7}{2}$,即为2<x<$\frac{7}{2}$;
当x≤2时,f(x)<1即-2<1,即有x≤2,
综上可得,解集为(2,$\frac{7}{2}$)∪(-∞,2]=(-∞,$\frac{7}{2}$);
(Ⅱ)函数f(x)=|x-2|-|x-a|,(a<0),
|f(x)|=||x-2|-|x-a||≤|(x-2)-(x-a)|=2-a,
即有f(x)的最大值为2-a,
不等式|f(x)|<a2恒成立,即有a2>2-a,
解得a>1或a<-2,又a<0,
则a<-2.
即有a的取值范围是(-∞,-2).
点评 本题考查绝对值不等式的解法,主要考查分类讨论的思想方法和绝对值不等式的性质的运用,注意恒成立思想方法转化为求函数的最值问题,属于中档题和易错题.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
20.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一个焦点F1作一条渐近线的垂线,垂足为A,与另一条渐近线交于点B,若A恰好是F1B的中点,则双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
18.阅读下列算法:
(1)输入x.
(2)判断x>2是否成立,若是,y=x; 否则,y=-2x+6.
(3)输出y.
当输入的x∈[0,7]时,输出的y的取值范围是( )
(1)输入x.
(2)判断x>2是否成立,若是,y=x; 否则,y=-2x+6.
(3)输出y.
当输入的x∈[0,7]时,输出的y的取值范围是( )
| A. | [2,7] | B. | [2,6] | C. | [6,7] | D. | [0,7] |
5.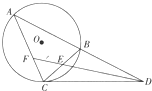 如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.
如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.
(Ⅰ)若∠ADC的平分线分别交BC、AC于点E、F,求证:CE=CF;
(Ⅱ)若CD=6,BC=5,求线段AC的长.
 如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.
如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.(Ⅰ)若∠ADC的平分线分别交BC、AC于点E、F,求证:CE=CF;
(Ⅱ)若CD=6,BC=5,求线段AC的长.
19.已知下表所示数据的回归直线方程为 $\widehaty$=4x+242.则实数a=262
| X | 2 | 3 | 4 | 5 | 6 |
| y | 251 | 254 | 257 | a | 266 |