题目内容
6.设g(x)=$\left\{\begin{array}{l}{{e}^{x}}&{x≤0}\\{lnx}&{x>0}\end{array}\right.$,则g(e-1)=-1.分析 由g(x)=$\left\{\begin{array}{l}{{e}^{x}}&{x≤0}\\{lnx}&{x>0}\end{array}\right.$,将x=e-1代入可得答案.
解答 解:∵g(x)=$\left\{\begin{array}{l}{{e}^{x}}&{x≤0}\\{lnx}&{x>0}\end{array}\right.$,e-1>0,
∴g(e-1)=ln(e-1)=-1,
故答案为:-1.
点评 本题考查的知识点是分段函数的应用,函数求值,难度不大,属于基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知点O在△ABC内部一点,且满足2$\overrightarrow{OA}$+3$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$,则三角形△AOB,△BOC,△AOC的面积之比依次为( )
| A. | 4:2:3 | B. | 2:3:4 | C. | 4:3:2 | D. | 3:4:5 |
17.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若A=60°,c=4,a=4,则此三角形有( )
| A. | 两解 | B. | 一解 | C. | 无解 | D. | 无穷多解 |
1.如图给定的是纸盒的外表面,下列哪一项能由它折叠而成( )


| A. | 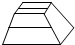 | B. |  | C. |  | D. | 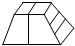 |