题目内容
已知等比数列{an}公比为q,其前n项和为Sn,若S3,S9,S6成等差数列,则q3等于
A.- | B.1 | C.- 或1 或1 | D.-1或 |
A
解析试题分析:因为S3,S9,S6成等差数列,即,2S9=S6 +S3,所以2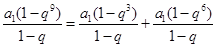 ,整理得,
,整理得,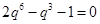 ,解得q3=
,解得q3=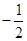 或1,但q3=1时与已知不符,故选A。
或1,但q3=1时与已知不符,故选A。
考点:本题主要考查等比数列通项公式、求和公式。
点评:简单题,根据S3,S9,S6成等差数列可建立q的方程,解之即得。

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
若等比数列{a }的前三项和为13,首项为1,则其公比为
}的前三项和为13,首项为1,则其公比为
| A.2或-1 | B.3或-4 | C.4或-3 | D.3 |
各项都为正数的数列 中,
中, 猜想数列
猜想数列 的通项
的通项
A. | B. | C. | D. |
已知a,b,a+b成等差数列,a,b,ab成等比数列,且0<log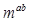 <1,则m的取值范围是( )
<1,则m的取值范围是( )
| A.m>1 | B.1<m<8 |
| C.m>8 | D.0<m<1或m>8 |
设 成等比数列,其公比为2,则
成等比数列,其公比为2,则 的值为( )
的值为( )
A. | B. | C. | D.1 |
若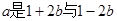 的等比中项,则
的等比中项,则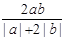 的最大值为( )
的最大值为( )
A.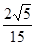 | B.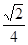 | C.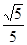 | D.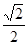 |
已知点 (
( ,
, )(
)( N*)都在函数
N*)都在函数 (
( )的图象上,则
)的图象上,则 与
与 的大小关系是( )
的大小关系是( )
A. > > | B. < < |
C. = = | D. 与 与 的大小与 的大小与 有关 有关 |
等比数列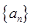 中,
中,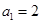 ,
, =4,函数
=4,函数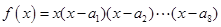 ,则
,则 ( )
( )
A.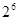 | B.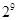 | C.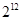 | D. |
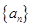 中,
中, ,
, ,
, ,则
,则 ( )
( )