题目内容
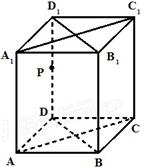 (2010•青浦区二模)已知ABCD-A1B1C1D1是底面为菱形的直四棱柱,P是棱DD1的中点,∠BAD=60°,底面边长为2,四棱柱的体积为8
(2010•青浦区二模)已知ABCD-A1B1C1D1是底面为菱形的直四棱柱,P是棱DD1的中点,∠BAD=60°,底面边长为2,四棱柱的体积为8| 3 |
分析:通过体积求出几何体的高,取AD的中点为E,连接PE,PB,说明∠EPB为直线PB与直线AD1所成的角,然后解三角形求出sin∠EPB,异面直线AD1与PB所成的角大小.
解答:解:由体积为8
,得h×2×2sin60°=8
,所以h=4(3分)
则BE⊥ADD1A1,(5分)
AD1∥PE,∠EPB为直线PB与直线AD1所成的角.(8分)
经计算BE=
,PB=2
,(10分)
sin∠EPB=
=
,
即异面直线AD1与PB所成的角为arcsin
(或arctan
).(12分)
| 3 |
| 3 |
则BE⊥ADD1A1,(5分)
AD1∥PE,∠EPB为直线PB与直线AD1所成的角.(8分)
经计算BE=
| 3 |
| 2 |
sin∠EPB=
| ||
2
|
| ||
| 4 |
即异面直线AD1与PB所成的角为arcsin
| ||
| 4 |
| ||
| 5 |
点评:本题考查异面直线及其所成的角,考查计算能力,逻辑思维能力,是基础题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目