题目内容
(本小题12分)已知函数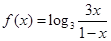 .
.
(1)证明函数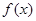 的图像关于点
的图像关于点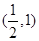 对称;
对称;
(2)若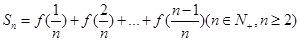 ,求
,求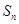 ;
;
(3)在(2)的条件下,若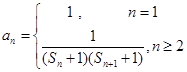
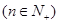 ,
,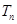 为数列
为数列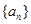 的前
的前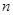 项和,若
项和,若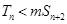 对一切
对一切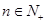 都成立,试求实数
都成立,试求实数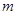 的取值范围.
的取值范围.
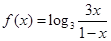 .
. (1)证明函数
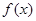 的图像关于点
的图像关于点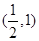 对称;
对称;(2)若
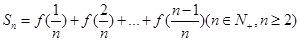 ,求
,求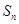 ;
;(3)在(2)的条件下,若
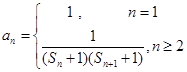
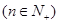 ,
,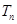 为数列
为数列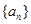 的前
的前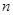 项和,若
项和,若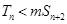 对一切
对一切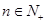 都成立,试求实数
都成立,试求实数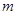 的取值范围.
的取值范围.(1) 证明:见解析;(2) ;(3)
;(3)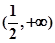 .
.
 ;(3)
;(3)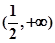 .
.(1)证明f(x)关于点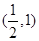 对称,只须证明:设
对称,只须证明:设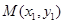 、
、 是函数
是函数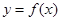 图像上的两点, 其中
图像上的两点, 其中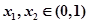 且
且 ,即证:
,即证: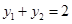 即可.
即可.
(2)利用(1)的结论,采用倒序相加的方法求和即可。
(3)当 时,
时, , 当
, 当 时,
时, ,
,  .可求出
.可求出
然后再本小题可转化为 对一切
对一切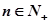 都成立,即
都成立,即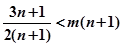 恒成立,又即
恒成立,又即
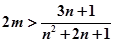 恒成立,再构造
恒成立,再构造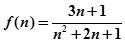 ,研究其最大值即可。
,研究其最大值即可。
(1) 证明:因为函数 的定义域为
的定义域为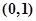 , 设
, 设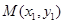 、
、 是函数
是函数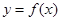 图像上的两点, 其中
图像上的两点, 其中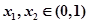 且
且 ,
,
则有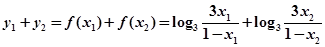
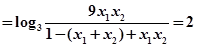
因此函数图像关于点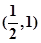 对称 ……………………………………4分
对称 ……………………………………4分
(2)由(1)知当 时,
时,
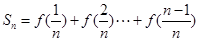 ①
①  ②
②
①+②得 ………………………………………………………………8分
………………………………………………………………8分
(3)当 时,
时,
当 时,
时, ,
, 
当 时,
时, …
…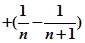 =
= 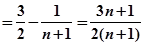
∴ (
(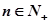 )
)
又 对一切
对一切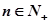 都成立,即
都成立,即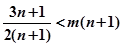 恒成立
恒成立
∴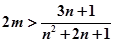 恒成立,又设
恒成立,又设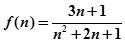 ,
, 所以
所以 在
在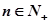 上递减,所以
上递减,所以 在
在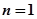 处取得最大值
处取得最大值
∴ ,即
,即
所以 的取值范围是
的取值范围是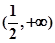 ………………12分
………………12分
 对称,只须证明:设
对称,只须证明:设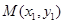 、
、 是函数
是函数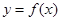 图像上的两点, 其中
图像上的两点, 其中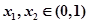 且
且 ,即证:
,即证: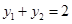 即可.
即可.(2)利用(1)的结论,采用倒序相加的方法求和即可。
(3)当
 时,
时, , 当
, 当 时,
时, ,
,  .可求出
.可求出
然后再本小题可转化为
 对一切
对一切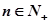 都成立,即
都成立,即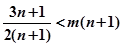 恒成立,又即
恒成立,又即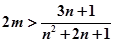 恒成立,再构造
恒成立,再构造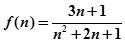 ,研究其最大值即可。
,研究其最大值即可。(1) 证明:因为函数
 的定义域为
的定义域为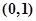 , 设
, 设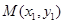 、
、 是函数
是函数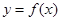 图像上的两点, 其中
图像上的两点, 其中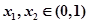 且
且 ,
,则有
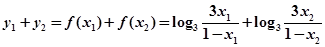
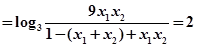
因此函数图像关于点
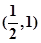 对称 ……………………………………4分
对称 ……………………………………4分 (2)由(1)知当
 时,
时,
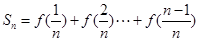 ①
①  ②
②①+②得
 ………………………………………………………………8分
………………………………………………………………8分(3)当
 时,
时,
当
 时,
时, ,
, 
当
 时,
时, …
…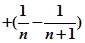 =
= 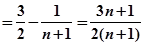
∴
 (
(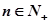 )
)又
 对一切
对一切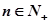 都成立,即
都成立,即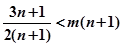 恒成立
恒成立∴
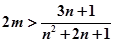 恒成立,又设
恒成立,又设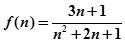 ,
, 所以
所以 在
在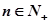 上递减,所以
上递减,所以 在
在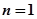 处取得最大值
处取得最大值
∴
 ,即
,即
所以
 的取值范围是
的取值范围是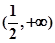 ………………12分
………………12分
练习册系列答案
相关题目
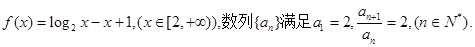
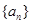 的通项公式
的通项公式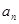 ;
;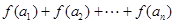 ;
; ,
,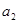 ,-1四个实数成等差数列,-4,
,-1四个实数成等差数列,-4,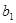 ,
,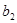 ,
,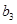 ,-1五个实数成
,-1五个实数成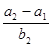 =
=  年比上一年增加
年比上一年增加 万吨,记2011年为第一年,甲、乙两工厂第
万吨,记2011年为第一年,甲、乙两工厂第 万吨和
万吨和 万吨.
万吨. ,
, 的通项公式;
的通项公式;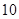 项的和为
项的和为 项的和为
项的和为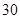 ,则前
,则前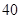 项的和为 ▲ .
项的和为 ▲ .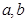 ,可按规则
,可按规则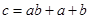 扩充为一个新数
扩充为一个新数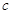 ,在
,在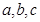 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.若
三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.若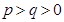 ,经过6次操作后扩充所得的数为
,经过6次操作后扩充所得的数为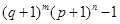 (
(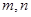 为正整数),则
为正整数),则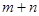 的值为 ▲ .
的值为 ▲ .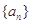 满足:所有的奇数项
满足:所有的奇数项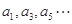 构成以1为首项,1为公差的等差数列;所有的偶数项
构成以1为首项,1为公差的等差数列;所有的偶数项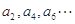 构成以2为首项,3为公差的等差数列,则
构成以2为首项,3为公差的等差数列,则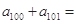 ( )
( )
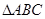 的三内角
的三内角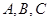 成等差数列,且
成等差数列,且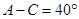 ,则
,则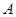 = .
= .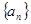 是各项正的等比数列,且
是各项正的等比数列,且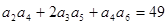 ,则
,则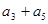 =
=