题目内容
已知向量 sinωx,cosωx),
sinωx,cosωx), ,记函数f(x)=
,记函数f(x)= ,已知f(x)的周期为π.
,已知f(x)的周期为π.(1)求正数ω之值;
(2)当x表示△ABC的内角B的度数,且△ABC三内角A、B、C满sin2B=sinA•sinC,试求f(x)的值域.
【答案】分析:(1)由题设条件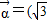 sinωx,cosωx),
sinωx,cosωx),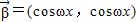 ,记函数f(x)=
,记函数f(x)=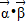 ,得到
,得到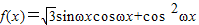 ,进行恒等变形,得到f(x)=
,进行恒等变形,得到f(x)=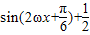 ,再由函数的周期公式求出正数ω之值;
,再由函数的周期公式求出正数ω之值;
(2)且△ABC三内角A、B、C满sin2B=sinA•sinC,得出b2=ac,结合余弦定理求出cosB的取值范围,即得函数的定义域,再求f(x)的值域
解答:解:(1)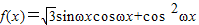 =
=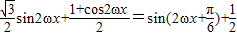 ,
,
因为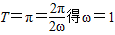 .
.
(2)由(1)得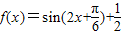 ,由sin2B=sinA•sinC得b2=ac
,由sin2B=sinA•sinC得b2=ac
又b2=a2+c2-2accosB,∴ ,∴
,∴ ,∴
,∴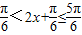 ,∴
,∴ .
.
点评:本题考查余弦定理的应用,解题的关键是熟练掌握三角恒等变换公式以及三角函数周期公式,余弦定理,本题是三角函数在高考中的经典题型,综合考查了三角函数中的多个知识点,综合性强,考查了恒等变形的能力,转化的能力,及计算能力
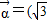 sinωx,cosωx),
sinωx,cosωx),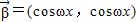 ,记函数f(x)=
,记函数f(x)=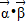 ,得到
,得到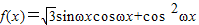 ,进行恒等变形,得到f(x)=
,进行恒等变形,得到f(x)=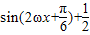 ,再由函数的周期公式求出正数ω之值;
,再由函数的周期公式求出正数ω之值;(2)且△ABC三内角A、B、C满sin2B=sinA•sinC,得出b2=ac,结合余弦定理求出cosB的取值范围,即得函数的定义域,再求f(x)的值域
解答:解:(1)
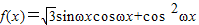 =
=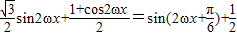 ,
,因为
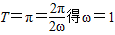 .
.(2)由(1)得
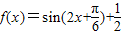 ,由sin2B=sinA•sinC得b2=ac
,由sin2B=sinA•sinC得b2=ac又b2=a2+c2-2accosB,∴
 ,∴
,∴ ,∴
,∴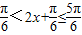 ,∴
,∴ .
.点评:本题考查余弦定理的应用,解题的关键是熟练掌握三角恒等变换公式以及三角函数周期公式,余弦定理,本题是三角函数在高考中的经典题型,综合考查了三角函数中的多个知识点,综合性强,考查了恒等变形的能力,转化的能力,及计算能力

练习册系列答案
相关题目
 sinωx,cosωx),
sinωx,cosωx), ,记函数f(x)=
,记函数f(x)= ,已知f(x)的周期为π.
,已知f(x)的周期为π. sinωx,cosωx),
sinωx,cosωx), ,记函数f(x)=
,记函数f(x)= ,已知f(x)的周期为π.
,已知f(x)的周期为π.