题目内容
【题目】某校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩，被抽取学生的成绩均不低于160分，且低于185分，如图是按成绩分组得到的频率分布直方图．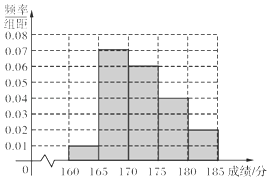 
（1）为了能选拔出优秀的学生，该校决定在笔试成绩较高的第3组、第4组、第5组中用分层抽样的方法抽取6名学生进入第二轮面试，求第3，4，5组每组各抽取多少名学生进入第二轮面试；
（2）在（1）的前提下，学校决定在6名学生中随机抽取2名学生由考官A面试，求第4组至少有一名学生被考官A面试的概．
【答案】
（1）解：第3，4，5组共60人，用分层抽样抽取6人．
故第3，4，5组中应抽取的学生人数依次为：
第3组： 
×6=3（人）；第4组 
×6=2（人）；第5组： 
×6=1（人）．
（2）解：设第3组的3位同学为A1，A2，A3，
第4组的2位同学为B1，B2，第5组的1位同学为C，
则从六位同学中抽取两位同学有15种可能如下：
（A1，A2），（A1，A3），（A1，B1），（A1，B2），（A1，C），
（A2，A3），（A2，B1），（A2，B2），（A2，C），（A3，B1），
（A3，B2），（A3，C），（B1，B2），（B1，C），（B2，C）．
而满足题意的情况有：
（A1，B1），（A1，B2），（A2，B1），（A2，B2，（A3，B1，
（A3，B2），（B1，B2），（B1，C），（B2，C）共9种．
因此所求事件的概率为 
= 
【解析】（1）根据分层抽样的比例计算即可；（2）列出满足条件的情况，从而求出其概率．
【考点精析】本题主要考查了频率分布直方图的相关知识点，需要掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息才能正确解答此题．
