题目内容
数列1,1+2,1+2+22,…,1+2+22+…+2n-1,…的前n项和为( )
| A.2n-n-1 | B.2n+1-n-2 |
| C.2n | D.2n+1-n |
B
因为根据题意可知,1+2+22+…+2n-1=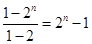 ,因此通项公式是由等差数列和等比数列的和,利用等比数列和等差数列的前n项和得到和式为2n+1-n-2,选B.
,因此通项公式是由等差数列和等比数列的和,利用等比数列和等差数列的前n项和得到和式为2n+1-n-2,选B.
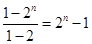 ,因此通项公式是由等差数列和等比数列的和,利用等比数列和等差数列的前n项和得到和式为2n+1-n-2,选B.
,因此通项公式是由等差数列和等比数列的和,利用等比数列和等差数列的前n项和得到和式为2n+1-n-2,选B.
练习册系列答案
相关题目
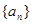 的首项为
的首项为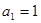 ,前n项和
,前n项和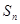 满足关系式:
满足关系式: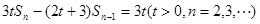
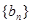 ,使得
,使得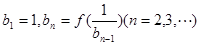 ,求:b
,求:b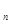 及
及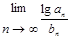 ;
;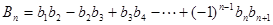 。
。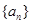 中,若
中,若 ,则
,则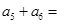
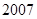 年
年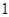 月
月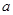 元,若按年利率为
元,若按年利率为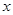 ,并按复利计算,到
,并按复利计算,到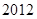 年
年 元
元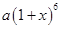 元
元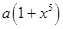 元
元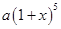 元
元 项和为
项和为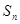 ,若
,若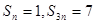 ,则
,则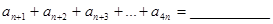
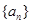 是公比大于1的等比数列,
是公比大于1的等比数列,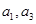 是函数
是函数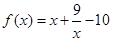 的两个零点。
的两个零点。 满足
满足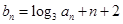 ,且
,且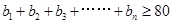 ,求
,求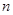 的最小值。
的最小值。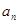 }满足
}满足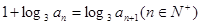 ,且
,且 ,则
,则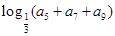 的值是 ( )
的值是 ( )

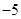
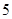
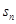 为等比数列
为等比数列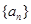 的前n项和,
的前n项和,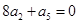 则
则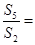
 ( )
( )