已知曲线C的极坐标方程是ρ=2sinθ.设直线l的参数方程是x=-3t+2y=4t.试判断直线l和曲线C的位置关系．题目和参考答案——青夏教育精英家教网—

题目内容

已知曲线C的极坐标方程是ρ=2sinθ，设直线l的参数方程是

x=-3t+2

y=4t

（t为参数），试判断直线l和曲线C的位置关系．

分析：将曲线C的极坐标方程化为直角坐标方程后，发现曲线C为圆，找出圆心坐标和圆的半径，又把直线l的参数方程化为普通方程后，利用点到直线的距离公式求出圆心到直线l的距离d与圆的半径r比较大小即可判断出直线l和曲线C的位置关系．

解答：解：将曲线C的极坐标方程化为直角坐标方程得x²+y²-2y=0，
故知曲线C为圆，其圆心坐标为（0，1），半径r=1．
将直线l的参数方程化为普通方程得：4x+3y-8=0．
由于圆心到直线l的距离d=

|3×1-8|

42+32

=1=r，
故直线l与圆C相切．

点评：此题考查学生会将极坐标方程和参数方程分别化为直角坐标方程和普通方程，掌握直线与圆位置关系的判断方法，灵活运用点到直线的距离公式化简求值，是一道中档题．

练习册系列答案

相关题目

2、已知曲线C的极坐标方程是ρ=4cosθ，那么它的直角坐标方程是

（x-2）²+y²=4

．

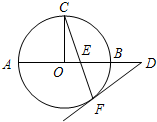A（选修4-1：几何证明选讲）
如图，AB是⊙O的直径，C，F是⊙O上的两点，OC⊥AB，过点F作⊙O的切线FD交AB的延长线于点D，连接CF交AB于点E．
求证：DE²=DB•DA．
B（选修4-2：矩阵与变换）
求矩阵

2	1
1	2

的特征值及对应的特征向量．
C（选修4-4：坐标系与参数方程）
已知曲线C的极坐标方程是ρ=2sinθ，直线l的参数方程是

x=-

t+2

（t为参数）．
（Ⅰ）将曲线C的极坐标方程化为直角坐标方程；
（Ⅱ）设直线l与x轴的交点是M，N是曲线C上一动点，求MN的最大值．
D（选修4-5：不等式选讲）
已知m＞0，a，b∈R，求证：(

．

（坐标系与参数方程选做题）．
已知曲线C的极坐标方程是ρ=1，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是

x=-1+4t

y=3t

（t为参数），则直线l与曲线C相交所成的弦的弦长为

．

（2013•文昌模拟）选修4-4：坐标系与参数方程
已知曲线C的极坐标方程是ρ=1，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程

x=1+

y=2+

(t为参数)．
（1）写出直线l的普通方程与曲线C的直角坐标方程；
（2）设曲线C经过伸缩变换

x′=3x

y′=y

得到曲线C′，设曲线C′上任一点为M（x，y），求x+2

y的最小值．

（坐标系与参数方程选做题）
已知曲线C的极坐标方程是ρ=6sinθ，以极点为坐标原点，极轴为x的正半轴，建立平面直角坐标系，直线l的参数方程是

t-1

(t为参数），则直线l与曲线C相交所得的弦的弦长为

．

试题分类