题目内容
在 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
.
(1)求 的值;
的值;
(2)若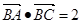 ,且
,且 ,求
,求 和
和 的值.
的值.
 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
.(1)求
 的值;
的值;(2)若
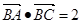 ,且
,且 ,求
,求 和
和 的值.
的值.(1)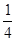 ;(2)
;(2)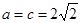 .
.
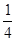 ;(2)
;(2)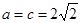 .
.试题分析:(1)有正弦定理把
 转化为
转化为
 ,再利用两个角的和的正弦公式
,再利用两个角的和的正弦公式 ,利用三角形三内角和定理
,利用三角形三内角和定理变形求得
 的值;(2)根据条件,利用向量的数量积公式结合(1)的结论,求得
的值;(2)根据条件,利用向量的数量积公式结合(1)的结论,求得 ,利用余弦定理
,利用余弦定理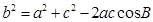 求得
求得 ,从而得出结论.
,从而得出结论.试题解析:(1)由正弦定理得
 ,
,则
 2分
2分故
 ,
,可得
 ,
,即
 ,
,可得
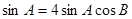 , 4分
, 4分又由
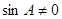 可得
可得 . 6分
. 6分(2)由
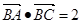 ,可得
,可得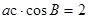 ,
,又因为
 ,
,故
 , 8分
, 8分又
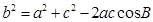 ,
,可得
 , 10分
, 10分所以
 ,即
,即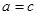 .
.所以
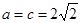 . 12分
. 12分
练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 的内角A、B、C所对的边为
的内角A、B、C所对的边为 ,
,  ,
,  ,且
,且 与
与 所成角为
所成角为 .
. 的取值范围.
的取值范围.
 求
求 的值域;
的值域; 求
求 的值.
的值.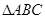 的内角
的内角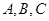 所对的边长分别为
所对的边长分别为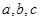 ,且满足
,且满足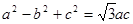
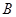 的大小;
的大小;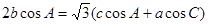 ,
,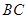 边上的中线
边上的中线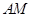 的长为
的长为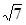 ,求
,求 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 .
. 的大小;
的大小; ,
, ,求a,c,的值.
,求a,c,的值. absin C,则△ABC的形状是( )
absin C,则△ABC的形状是( )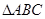 中,
中,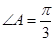 ,
,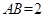 ,且
,且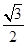 ,则边
,则边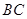 的长为_________.
的长为_________. ,
, ,则A=
,则A=  的内角
的内角 对边分别为
对边分别为 且
且 则
则 =( )
=( )