题目内容
设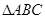 的内角
的内角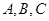 所对的边长分别为
所对的边长分别为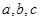 ,且满足
,且满足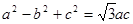
(Ⅰ)求角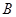 的大小;
的大小;
(Ⅱ)若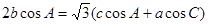 ,
,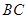 边上的中线
边上的中线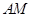 的长为
的长为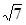 ,求
,求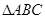 的面积.
的面积.
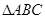 的内角
的内角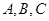 所对的边长分别为
所对的边长分别为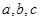 ,且满足
,且满足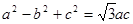
(Ⅰ)求角
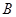 的大小;
的大小;(Ⅱ)若
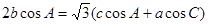 ,
,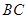 边上的中线
边上的中线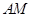 的长为
的长为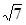 ,求
,求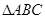 的面积.
的面积.(Ⅰ)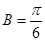 ;(Ⅱ)
;(Ⅱ)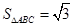 .
.
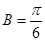 ;(Ⅱ)
;(Ⅱ)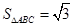 .
.试题分析:(Ⅰ)求角
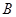 的大小,由于三角形的三边满足
的大小,由于三角形的三边满足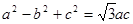 ,含有平方关系,可考虑利用余弦定理来解,由余弦定理得
,含有平方关系,可考虑利用余弦定理来解,由余弦定理得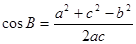 ,把
,把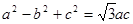 代入,可求得
代入,可求得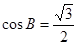 ,从而可得角
,从而可得角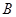 的值;(Ⅱ)由于
的值;(Ⅱ)由于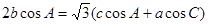 ,关系式中,即含有边,又含有角,需要进行边角互化,由于
,关系式中,即含有边,又含有角,需要进行边角互化,由于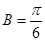 ,故利用正弦定理把边化成角,通过三角恒等变换求出
,故利用正弦定理把边化成角,通过三角恒等变换求出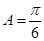 ,得三角形为等腰三角形,由于
,得三角形为等腰三角形,由于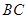 边上的中线
边上的中线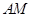 的长为
的长为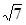 ,可考虑利用余弦定理来求
,可考虑利用余弦定理来求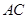 的长,由于
的长,由于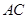 的长与
的长与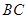 的长相等,又因为
的长相等,又因为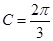 ,从而可求出
,从而可求出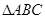 的面积.
的面积.试题解析:(Ⅰ)因为
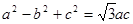 ,由余弦定理有
,由余弦定理有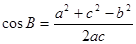 ,故有
,故有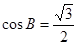 ,又
,又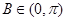 ,即:
,即: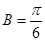 5分
5分(Ⅱ)由正弦定理:
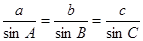 6分
6分可知:
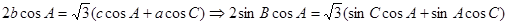
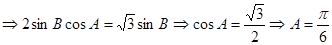 9分
9分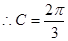 ,设
,设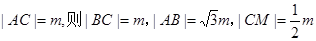 10分
10分由余弦定理可知:
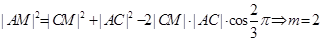 11分
11分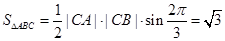 . 12分
. 12分
练习册系列答案
相关题目
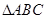 中,内角
中,内角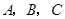 的对边分别为
的对边分别为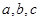 ,且
,且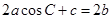 .
.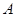 的大小;
的大小;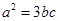 ,求
,求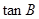 的值.
的值. 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
. 的值;
的值;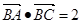 ,且
,且 ,求
,求 和
和 的值.
的值.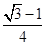 ,求C.
,求C. 中,内角
中,内角 所对的边分别是
所对的边分别是 ,已知
,已知 .
. ,
, ,求
,求 ,
, ,求
,求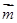 =(
=(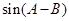 ,
,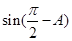 ),
),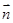 =(1,
=(1,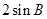 ),且
),且
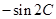 ,其中
,其中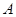 、
、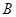 、
、 分别为
分别为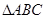 的三边
的三边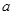 、
、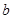 、
、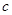 所对的角.
所对的角.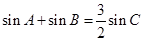 ,且
,且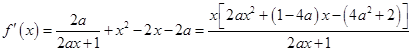 ,求边
,求边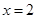 的长.
的长.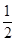 b,且a>b,则∠B=( )
b,且a>b,则∠B=( )



 中,
中, ,
, ,
, ,则
,则 .
. 中,若
中,若 ,面积记作
,面积记作 ,则下列结论中一定成立的是( )
,则下列结论中一定成立的是( )


