题目内容
【题目】已知动点 
到点 
的距离比它到直线 
的距离小 
，记动点 的轨迹为 
.若以 
为圆心， 
为半径（ 
）作圆，分别交 
轴于 
两点，连结并延长 
，分别交曲线 于 
两点.
（1）求曲线 的方程；
（2）求证：直线 
的斜率为定值.
【答案】
（1）解：动点 
到点 
的距离比它到直线 
的距离小 
，可得动点 到点 的距离与它到直线 
的距离相等，由定义可得曲线 
方程为 
（2）解：设 
， 
与抛物线方程 联立得： 
， 
由题意有 
， 
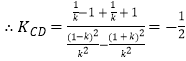
【解析】本题考查抛物线方程的求法，考查两直线的斜率的比值是否为定值的判断与求法，解题时要认真审题，注意直线方程的合理运用．
【考点精析】认真审题，首先需要了解抛物线的定义(平面内与一个定点
和一条定直线
的距离相等的点的轨迹称为抛物线．定点称为抛物线的焦点，定直线称为抛物线的准线)．
练习册系列答案
阅读快车系列答案
相关题目
【题目】为了引导居民合理用水，某市决定全面实施阶梯水价，阶梯水价原则上以住宅（一套住宅为一户）的月用水量为基准定价，具体划分标准如表：
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围（单位：立方米） | （0，10] | （10，15] | （15，+∞） |
从本市随机抽取了10户家庭，统计了同一个月的用水量，得到如图所示的茎叶图．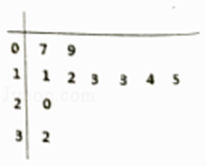
（1）现要在这10户家庭中任意选取3户，求取到第二阶梯水量的户数的分布列和均值；
（2）用抽到的10户家庭作为样本估计全市的居民用水情况，从全市依次随机抽取10户，若抽到n户月用水量为第二阶梯水量的可能性最大，求出n的值．
