��Ŀ����
����Ŀ�������ݡ��ŷɴ����ز�˳����������Ϊ�˼�ʱ������Ա�ȳ�������ָ�������ڷ��ز�Ԥ�Ƶ������������ͬһ��ֱ���ϵ�������Ԯ���ģ���ΪB��C��D���������زվ����1����P��ʱ���ٶ��Ժ�ֱ���䣬����A����½����C��Ԯ���IJ�÷ɴ�λ������ƫ��60�㷽������Ϊ60�㣬B��Ԯ���IJ�÷ɴ�λ������ƫ��30�㷽������Ϊ30�㣮D��Ԯ���IJ����½��Aλ������������
��1����B��C����Ԯ���ļ�ľ��룻
��2��D��Ԯ��������½��A��ľ��룮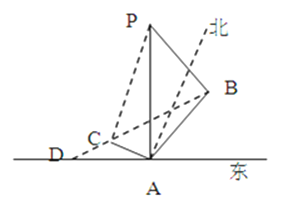
���𰸡��⣺��1��������֪PA��AC��PA��AB�����PAC����PAB��Ϊֱ��������
��Rt��PAC�У�PA=1����PCA=60�㣬���AC=![]()
��Rt��PAB�У�PA=1����PBA=30�㣬���AB=![]()
�֡�CAB=90�㣬BC=![]() ����
����
��2��![]() ��
��
�֡�CAD=30�㣬����![]()
�ڡ�ADC�У������Ҷ�����![]()
AD=![]() ����
����
����������1�����������֪��PAC����PAB��Ϊֱ�������Σ������ֱ����������������������е�һ�Ǻ�һ�����AC��AB��������ù��ɶ������BC��
��2��������ͬ�����Ǻ����Ļ�����ϵ���cos��ACD����������sin��ADC=sin��30��+��ACD���������Ǻ�ʽ���sin��ADC������������Ҷ������AD��