题目内容
(本题14分)已知向量![]() 动点
动点![]() 到定直线
到定直线![]() 的距离等于
的距离等于![]() 并且满足
并且满足![]() 其中
其中![]() 是坐标原点,
是坐标原点,![]() 是参数.
是参数.
(1)求动点![]() 的轨迹方程,并判断曲线类型;
的轨迹方程,并判断曲线类型;
(2)当![]() 时,求
时,求![]() 的最大值和最小值;
的最大值和最小值;
(3)如果动点![]() 的轨迹是圆锥曲线,其离心率
的轨迹是圆锥曲线,其离心率![]() 满足
满足![]() 求实数
求实数![]() 的取值范围。
的取值范围。
解:(1)设![]() 由题设可得
由题设可得![]()
![]()
![]() ,
,
因![]()
![]()
即![]() 为所求轨迹方程。 ---------------(2分)
为所求轨迹方程。 ---------------(2分)
当![]() 时,
时,![]() 动点
动点![]() 的轨迹是一条直线;
的轨迹是一条直线;
当![]() 时,
时,![]() 动点
动点![]() 的轨迹是圆;
的轨迹是圆;
当![]() 时,方程可化为
时,方程可化为![]() 当
当![]() 时,动点
时,动点![]() 的轨迹是双曲线;
的轨迹是双曲线;
当![]() 时,动点
时,动点![]() 的轨迹是椭圆。 -------------------(6分)
的轨迹是椭圆。 -------------------(6分)
(2)当![]() 时,
时, ![]() 的轨迹方程为
的轨迹方程为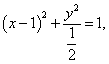 得
得![]()
![]()
![]()
![]()
∴当![]() 时,
时,![]() 取最小值
取最小值![]()
当![]() 时,
时,![]() 取最大值16.
取最大值16.
因此,![]() 的最小值是
的最小值是![]() ,最大值是4. ----------------(10分)
,最大值是4. ----------------(10分)
(3)由于![]() 即
即![]() 此时圆锥曲线是椭圆,其方程可化为
此时圆锥曲线是椭圆,其方程可化为![]()
①当![]() 时,
时,![]()
![]()
![]() ------------------- (12分)
------------------- (12分)
②当![]() 时,
时,![]()
![]()
![]() 而
而![]() 得,
得,![]()
综上,![]() 的取值范围是
的取值范围是 ![]() ---------------(14分)
---------------(14分) www..com
www..com

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
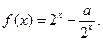 将
将 的图象向右平移2个单位,得到
的图象向右平移2个单位,得到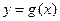 的图象.
的图象.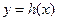 与函数
与函数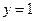 对称,求函数
对称,求函数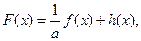 已知
已知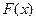 的最小值是
的最小值是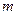 ,且
,且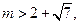 求实数
求实数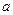 的
的 取值范围.
取值范围.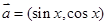 ,
,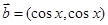 ,
,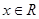 ,函数
,函数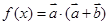
 的最大值与最小正周期;
的最大值与最小正周期; 成立的
成立的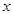 的取值集合.
的取值集合.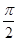 个单位,再把图象所有点的横坐标缩短到原来的
个单位,再把图象所有点的横坐标缩短到原来的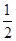 倍得到
倍得到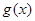 ,关于
,关于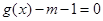 在
在 有且仅有一个解,求
有且仅有一个解,求 的取值范围。
的取值范围。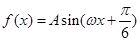 (其中
(其中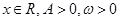 )的图象与
)的图象与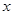 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为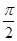 ,且图象上一个点为
,且图象上一个点为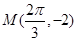 .
.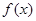 的解析式;
的解析式;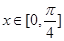 求函数
求函数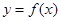 的图象向左平移
的图象向左平移 (a>b>0)的离心率为
(a>b>0)的离心率为 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3.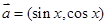 ,
,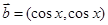 ,
,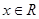 ,函数
,函数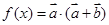
 的最大值与最小正周期;
的最大值与最小正周期;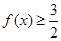 成立的
成立的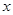 的取值集合.
的取值集合.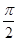 个单位,再把图象所有点的横坐标缩短到原来的
个单位,再把图象所有点的横坐标缩短到原来的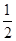 倍得到
倍得到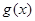 ,关于
,关于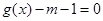 在
在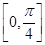 有且仅有一个解,求
有且仅有一个解,求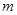 的取值范围。
的取值范围。