题目内容
设a、b、c分别是△ABC三个内角∠A、∠B、∠C的对边,若向量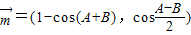 ,
,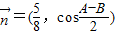 且
且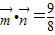 ,
,(1)求tanA•tanB的值;
(2)求
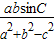 的最大值.
的最大值.
【答案】分析:(1)由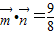 ,化简得 4cos(A-B)=5cos(A+B),由此求得tanA•tanB的值.
,化简得 4cos(A-B)=5cos(A+B),由此求得tanA•tanB的值.
(2)利用正弦定理和余弦定理化简为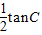 ,而
,而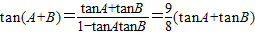 ,利用基本不等式
,利用基本不等式
求得它的最小值等于 ,从而得到tanC有最大值
,从而得到tanC有最大值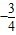 ,从而求得所求式子的最大值.
,从而求得所求式子的最大值.
解答:解:(1)由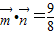 ,得
,得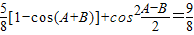 .…(2分)
.…(2分)
即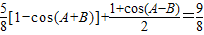 ,
,
亦即 4cos(A-B)=5cos(A+B),…(4分)
所以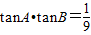 .…(6分)
.…(6分)
(2)因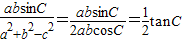 ,…(8分)
,…(8分)
而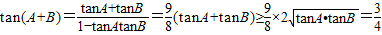 ,
,
所以,tan(A+B)有最小值 ,…(10分)
,…(10分)
当且仅当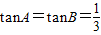 时,取得最小值.
时,取得最小值.
又tanC=-tan(A+B),则tanC有最大值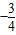 ,故
,故 的最大值为
的最大值为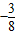 .…(13分)
.…(13分)
点评:本题主要考查两个向量数量积公式,正弦定理和余弦定理,两角和的正切公式,以及基本不等式的应用,属于中档题.
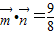 ,化简得 4cos(A-B)=5cos(A+B),由此求得tanA•tanB的值.
,化简得 4cos(A-B)=5cos(A+B),由此求得tanA•tanB的值.(2)利用正弦定理和余弦定理化简为
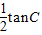 ,而
,而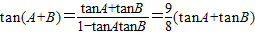 ,利用基本不等式
,利用基本不等式求得它的最小值等于
 ,从而得到tanC有最大值
,从而得到tanC有最大值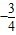 ,从而求得所求式子的最大值.
,从而求得所求式子的最大值.解答:解:(1)由
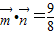 ,得
,得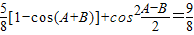 .…(2分)
.…(2分)即
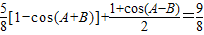 ,
,亦即 4cos(A-B)=5cos(A+B),…(4分)
所以
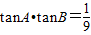 .…(6分)
.…(6分)(2)因
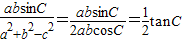 ,…(8分)
,…(8分)而
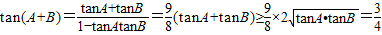 ,
,所以,tan(A+B)有最小值
 ,…(10分)
,…(10分) 当且仅当
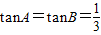 时,取得最小值.
时,取得最小值.又tanC=-tan(A+B),则tanC有最大值
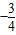 ,故
,故 的最大值为
的最大值为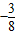 .…(13分)
.…(13分)点评:本题主要考查两个向量数量积公式,正弦定理和余弦定理,两角和的正切公式,以及基本不等式的应用,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
设a、b、c分别是方程2x=log
x,(
)x=log
x,(
)x=log2x的实数根,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、c<b<a |
| B、a<b<c |
| C、b<a<c |
| D、c<a<b |
设a、b、c分别是函数f(x)=(
)x-log2x,g(x)=2x-log
x,h(x)=(
)x-log
x的零点,则a、b、c的大小关系为( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、b<c<a |
| B、a<b<c |
| C、b<a<c |
| D、c<b<a |