题目内容
(2012•虹口区三模)已知圆G:x2+y2-2x-
y=0经过椭圆
+
=1(a>b>0)的右焦点F及上顶点B.
(1)求椭圆的方程;
(2)过椭圆外一点M(m,0)(m>a)倾斜角为
π的直线l交椭圆于C、D两点,若右焦点F在以线段CD为直径的圆E的外部,求m的取值范围.
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的方程;
(2)过椭圆外一点M(m,0)(m>a)倾斜角为
| 5 |
| 6 |
分析:(1)利用圆的方程,确定F,B的坐标,进而可得椭圆的方程;
(2)设直线l的方程与椭圆方程联立,利用韦达定理及右焦点F在以线段CD为直径的圆E的外部,建立不等式,即可确定m的取值范围.
(2)设直线l的方程与椭圆方程联立,利用韦达定理及右焦点F在以线段CD为直径的圆E的外部,建立不等式,即可确定m的取值范围.
解答:解:(1)∵圆G:x2+y2-2x-
y=0经过椭圆
+
=1(a>b>0)的右焦点F及上顶点B.
∴F(2,0),B(0,
)
∴c=2,b=
∴a2=6
∴椭圆的方程为
+
=1
(2)设直线l的方程为y=-
(x-m)(m>
)
由
得2x2-2mx+(m2-6)=0
由△=4m2-8(m2-6)>0,可得-2
<m<2
,
又m>
,∴
<m<2
(10分)
设C(x1,y1),D(x2,y2),则x1+x2=m,x1x2=
,
∴y1y2=[-
(x1-m)]•[-
(x2-m)]=
x1x2-
(x1+x2)+
∵
=(x1-2,y1),
=(x2-2,y2),
∴
•
=(x1-2)(x2-2)+y1y2=
x1x2-
(x1x2)+
+4=
∵点F在圆G的外部,∴
•
>0,即
>0,
解得m<0或m>3,又
<m<2
,
∴3<m<2
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
∴F(2,0),B(0,
| 2 |
∴c=2,b=
| 2 |
∴a2=6
∴椭圆的方程为
| x2 |
| 6 |
| y2 |
| 2 |
(2)设直线l的方程为y=-
| ||
| 3 |
| 6 |
由
|
由△=4m2-8(m2-6)>0,可得-2
| 3 |
| 3 |
又m>
| 6 |
| 6 |
| 3 |
设C(x1,y1),D(x2,y2),则x1+x2=m,x1x2=
| m2-6 |
| 2 |
∴y1y2=[-
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
| m |
| 3 |
| m2 |
| 3 |
∵
| FC |
| FD |
∴
| FC |
| FD |
| 4 |
| 3 |
| (m+6) |
| 3 |
| m2 |
| 3 |
| 2m(m-3) |
| 3 |
∵点F在圆G的外部,∴
| FC |
| FD |
| 2m(m-3) |
| 3 |
解得m<0或m>3,又
| 6 |
| 3 |
∴3<m<2
| 3 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,正确运用韦达定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
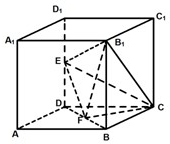 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点. (2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.
(2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.