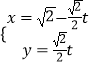题目内容
【题目】在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2BC,E,F,E1分别是棱AA1 , BB1 , A1B1的中点. 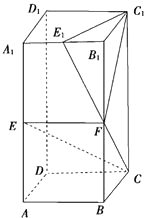
(1)求证:CE∥平面C1E1F;
(2)求证:平面C1E1F⊥平面CEF.
【答案】
(1)证明:取CC1的中点G,连接B1G交C1F于点F1,连接E1F1,A1G,FG,
∵F是BB1的中点,BCC1B1是矩形,
∵四边形FGC1B1也是矩形,
∴FC1与B1G相互平分,即F1是B1G的中点.
又E1是A1B1的中点,∴A1G∥E1F1.
又在长方体中,AA1綊CC1,E,G分别为AA1,CC1的中点,
∴A1E綊CG,∴四边形A1ECG是平行四边形,
∴A1G∥CE,∴E1F1∥CE.
∵CE平面C1E1F,E1F1平面C1E1F,
∴CE∥平面C1E1F
(2)证明:∵长方形BCC1B1中,BB1=2BC,F是BB1的中点,
∴△BCF、△B1C1F都是等腰直角三角形,
∴∠BFC=∠B1FC1=45°,
∴∠CFC1=180°﹣45°﹣45°=90°,
∴C1F⊥CF.
∵E,F分别是矩形ABB1A1的边AA1,BB1的中点,
∴EF∥AB.
又AB⊥平面BCC1B1,又C1F平面BCC1B1,
∴AB⊥C1F,∴EF⊥C1F.
又CF∩EF=F,∴C1F⊥平面CEF.
∵C1F平面C1E1F,∴平面C1E1F⊥平面CEF.
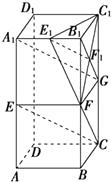
【解析】(1)要求证:CE∥平面C1E1F,取CC1的中点G,连接B1G交C1F于点F1,连接E1F1,A1G,FG,证明E1F1∥CE即可;(2)要证:平面C1E1F⊥平面CEF,证明C1F⊥CF,EF⊥C1F即可.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.