题目内容
已知函数 ,
,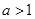 .
.
(1)讨论函数 的单调性;
的单调性;
(2)证明:若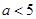 ,则对任意
,则对任意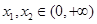 ,
,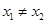 ,有
,有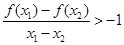 .
.
 ,
,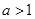 .
.(1)讨论函数
 的单调性;
的单调性; (2)证明:若
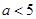 ,则对任意
,则对任意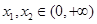 ,
,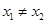 ,有
,有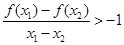 .
.(1) 在
在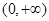 单调增加
单调增加
(2)见解析
 在
在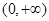 单调增加
单调增加(2)见解析
解:(1) 的定义域为
的定义域为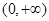 .
.
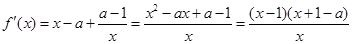 2分
2分
(1)若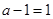 即
即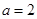 ,则
,则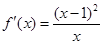 ,
,
故 在
在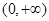 单调增加.
单调增加.
(2)若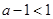 ,而
,而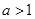 ,故
,故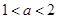 ,则当
,则当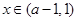 时,
时,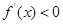 ;
;
当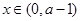 及
及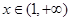 时,
时,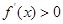 .故
.故 在
在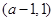 单调减少,
单调减少,
在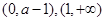 单调增加.
单调增加.
(iii)若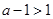 ,即
,即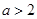 ,同理可得
,同理可得 在
在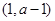 单调减少,在
单调减少,在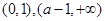 单调增加.
单调增加.
(2)考虑函数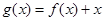
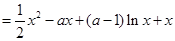 .
.
则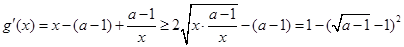 .
.
由于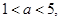 故
故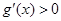 ,即
,即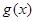 在
在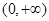 单调增加,从而当
单调增加,从而当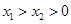 时有
时有
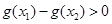 ,即
,即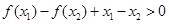 ,故
,故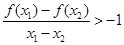 ,当
,当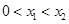 时,有
时,有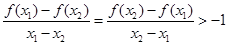 . 12分
. 12分
 的定义域为
的定义域为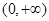 .
.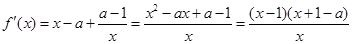 2分
2分(1)若
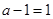 即
即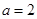 ,则
,则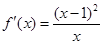 ,
,故
 在
在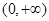 单调增加.
单调增加.(2)若
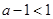 ,而
,而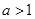 ,故
,故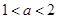 ,则当
,则当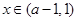 时,
时,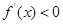 ;
;当
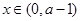 及
及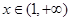 时,
时,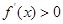 .故
.故 在
在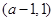 单调减少,
单调减少,在
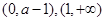 单调增加.
单调增加.(iii)若
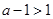 ,即
,即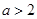 ,同理可得
,同理可得 在
在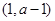 单调减少,在
单调减少,在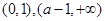 单调增加.
单调增加.(2)考虑函数
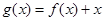
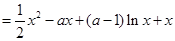 .
.则
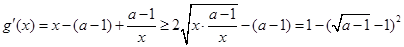 .
.由于
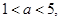 故
故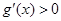 ,即
,即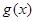 在
在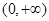 单调增加,从而当
单调增加,从而当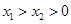 时有
时有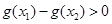 ,即
,即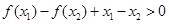 ,故
,故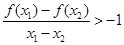 ,当
,当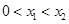 时,有
时,有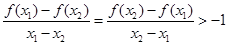 . 12分
. 12分
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
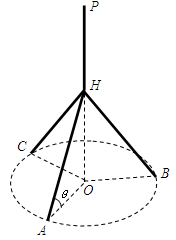
 构成,其底端三点
构成,其底端三点 均匀地固定在半径为
均匀地固定在半径为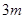 的圆
的圆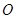 上(圆
上(圆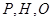 三点相异且共线,
三点相异且共线,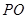 与地面垂直. 现要求点
与地面垂直. 现要求点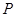 到地面的距离恰为
到地面的距离恰为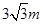 ,记用料总长为
,记用料总长为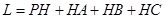 ,设
,设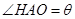 .
.
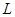 表示为
表示为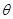 的函数,并注明定义域;
的函数,并注明定义域; 在
在 上是增函数.
上是增函数. 的取值范围
的取值范围 ;
;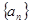 满足:
满足: ,且
,且 ,
, ,并判断
,并判断 与
与 的大小.
的大小.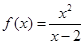 (x∈R,且x≠2).
(x∈R,且x≠2).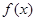 的单调区间;
的单调区间;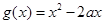 与函数
与函数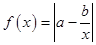 ,
, ,
,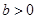 ,
,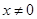 ,且满足:函数
,且满足:函数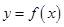 的图像与直线
的图像与直线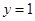 有且只有一个交点.
有且只有一个交点.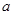 的值;
的值;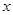 的不等式
的不等式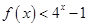 的解集为
的解集为 ,求实数
,求实数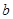 的值;
的值;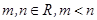 ,使得
,使得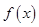 的定义域和值域均为
的定义域和值域均为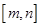 ,若存在,求出
,若存在,求出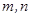 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.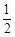 x
x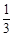 x
x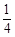 x
x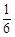 x
x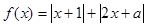 的最小值为3,则实数
的最小值为3,则实数 的值为( )
的值为( ) 或5
或5
 ,则
,则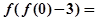 ;
;