题目内容
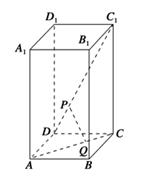
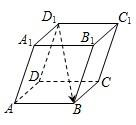
平行六面体ABCD-A1B1C1D1中,
=
,
=
,
=
,E,F为BD1,B1C1的中点,则
用
,
,
可表示为( )
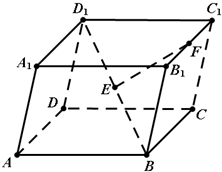
| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| EF |
| a |
| b |
| c |
A.
| B.
| C.-
| D.
|

平行六面体ABCD-A1B1C1D1中,
∵
=
,
=
,
=
,
且E,F为BD1,B1C1的中点,
∴
=
+
+
=
+
+
=
(
+
)+
+
=
(
+
+
)+
+
=
(-
-
+
)+
+
=
+
;
故选:B.
∵
| AB |
| a |
| AD |
| b |
| AA1 |
| c |
且E,F为BD1,B1C1的中点,
∴
| EF |
| EB |
| BB1 |
| B1F |
=
| 1 |
| 2 |
| D1B |
| AA1 |
| 1 |
| 2 |
| B1C1 |
=
| 1 |
| 2 |
| D1D |
| DB |
| c |
| 1 |
| 2 |
| AD |
=
| 1 |
| 2 |
| A1A |
| DA |
| AB |
| c |
| 1 |
| 2 |
| b |
=
| 1 |
| 2 |
| c |
| b |
| a |
| c |
| 1 |
| 2 |
| b |
=
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| c |
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形, ,
, 底面
底面 ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
 平面
平面 ;
; 与
与 所成角的大小;
所成角的大小; 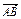 =a,
=a,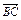 =b,
=b,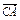 =c,且
=c,且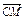 =3c,
=3c,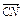 =-2b,
=-2b,