题目内容
已知点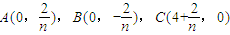
，其中n的为正整数．设Sn表示△ABC外接圆的面积，则
= ．
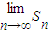【答案】分析：由三角形的对称性，先找出其外接圆圆心在X轴上，再求出半径，进而求出面积及其极限值．
解答：解：由题意可知外接圆圆心在X轴上，可设为O（a，0），则OA=OC，即OA2=OC2
∴
，
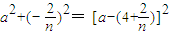解得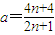
∴O为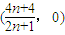
∴圆O的半径为OA=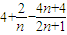
=
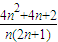
∴其外接圆的面积Sn=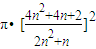
═
∴
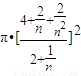
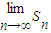=4π．
故答案是4π．
点评：本题的解答过程中，注意到先根据三角形的对称性找出外接圆圆心坐标，再进一步求解．
解答：解：由题意可知外接圆圆心在X轴上，可设为O（a，0），则OA=OC，即OA2=OC2
∴
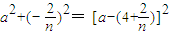，解得
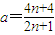
∴O为
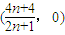
∴圆O的半径为OA=
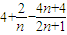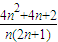
=∴其外接圆的面积Sn=
═∴
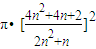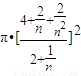
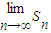=4π．故答案是4π．
点评：本题的解答过程中，注意到先根据三角形的对称性找出外接圆圆心坐标，再进一步求解．
练习册系列答案
备战中考寒假系列答案
相关题目
, 
，…
, 其中n是正整数. 对平面上任一点
, 记A1为A0关于点P1的对称点, A2为A1关于点P2的对称点, ┄, AN为AN-1关于点PN的对称点.
的坐标;
的图象,其中
是以3为周期的周期函数,且当x∈(0,3)时,
的坐标.
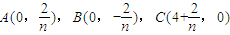，其中n的为正整数．设Sn表示△ABC外接圆的面积，则
= ．
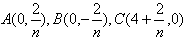，其中n的为正整数，设Sn表示△ABC外接圆的面积，则
=（ ）。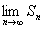