题目内容
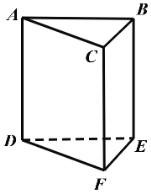
【题目】如图,一颗棋子从三棱柱的一个项点沿棱移到相邻的另一个顶点的概率均为![]() ,刚开始时,棋子在上底面点
,刚开始时,棋子在上底面点![]() 处,若移了
处,若移了![]() 次后,棋子落在上底面顶点的概率记为
次后,棋子落在上底面顶点的概率记为![]() .
.
(1)求![]() ,
,![]() 的值:
的值:
(2)求证:![]() .
.
【答案】(1)![]() ,
,![]() .(2)见解析
.(2)见解析
【解析】
(1)根据题意可知在上底面点![]() 处,移了
处,移了![]() 次可落在
次可落在![]() 的任意一点,可得
的任意一点,可得![]() ;分类讨论当第一次落在
;分类讨论当第一次落在![]() 或落在
或落在![]() 处的概率,即可得
处的概率,即可得![]() .
.
(2)根据移了![]() 次后棋子落在上底面顶点的概率为
次后棋子落在上底面顶点的概率为![]() ,可知落在下底面顶点的概率为
,可知落在下底面顶点的概率为![]() ,进而可得
,进而可得![]() 与
与![]() 的递推公式,利用构造数列法可得
的递推公式,利用构造数列法可得![]() 的通项公式;利用数学归纳法,即可证明
的通项公式;利用数学归纳法,即可证明![]() 成立.
成立.
(1)从三棱柱的一个项点沿棱移到相邻的另一个顶点的概率均为![]() ,棋子在上底面点
,棋子在上底面点![]() 处,移了
处,移了![]() 次可落在
次可落在![]() 的任意一点,
的任意一点,
所以![]() ,
,
若移![]() 次,则
次,则![]() 再移到上底面的概率为
再移到上底面的概率为![]() ,
,![]() 移到上底面的概率为
移到上底面的概率为![]() ,
,
所以![]() .
.
(2)证明:因为移了![]() 次后棋子落在上底面顶点的概率为
次后棋子落在上底面顶点的概率为![]() ,故落在下底面顶点的概率为
,故落在下底面顶点的概率为![]() .
.
于是移了![]() 次后棋子落在上底面顶点的概率为
次后棋子落在上底面顶点的概率为![]() .
.
从而![]() .
.
所以数列![]() 是等比数列,其首项为
是等比数列,其首项为![]() ,公比为
,公比为![]() .
.
所以![]() .
.
即![]() .用数学归纳法证明:
.用数学归纳法证明:
①当![]() 时,左式
时,左式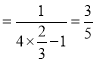 ,右式
,右式![]() ,因为
,因为![]() ,所以不等式成立.
,所以不等式成立.
当![]() 时,左式
时,左式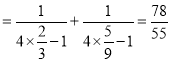 ,右式
,右式![]() ,因为
,因为![]() ,所以不等式成立.
,所以不等式成立.
②假设![]() 时,不等式成立,即
时,不等式成立,即![]() .
.
则![]() 时,左式
时,左式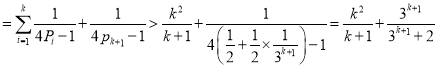 .
.
要证![]() ,只要证
,只要证![]() .
.
只要证![]() .
.
只要证![]() .
.
只要证![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() .即
.即![]() 时,不等式也成立.
时,不等式也成立.
由①②可知,不等式![]() 对任意的
对任意的![]() 都成立.
都成立.
不等式得证.

练习册系列答案
相关题目