题目内容
【题目】函数y=a2x+2ax-1(a>0且a≠1),当自变量x∈[-1,1]时,函数的最大值为14.试求a的值.
【答案】3或![]() .
.
【解析】试题分析:令ax=t,则函数可视为二次函数,根据条件确定定义域,再根据对称轴与定义区间位置关系讨论最大值取法,根据最大值为14列式解得a的值.
试题解析:y=(ax)2+2ax-1=(ax+1)2-2,
令ax=t,
∴y=(t+1)2-2.
当a>1时,
∵-1≤x≤1,
∴![]() ≤ax≤a,即
≤ax≤a,即![]() ≤t≤a.
≤t≤a.
∵函数的对称轴为t=-1,
∴当t=a时有最大值.
∴(a+1)2-2=14,∴a=3.
当0<a<1时,
∵-1≤x≤1,
∴a≤ax≤![]() .∴a≤t≤
.∴a≤t≤![]() .
.
∴当t=![]() 时有最大值,
时有最大值,
∴![]() 2-2=14.
2-2=14.
∴a=![]() .
.
∴a的值为3或![]() .
.

练习册系列答案
相关题目
【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
【题目】某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
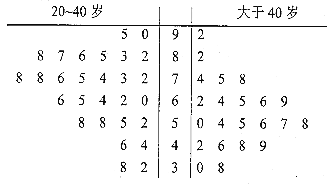
(1)根据茎叶图中的数据完成![]() 列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
购买意愿强 | 购买意愿弱 | 合计 | |
20~40岁 | |||
大于40岁 | |||
合计 |
(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,记抽到的2人中年龄大于40岁的市民人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() .
.