题目内容
(本小题12分)
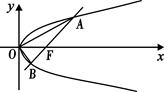
抛物线 上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|FA|=2,|FB|=5,(1)求直线AB的方程。
上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|FA|=2,|FB|=5,(1)求直线AB的方程。
(2)在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求这个最大面积.
抛物线
 上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|FA|=2,|FB|=5,(1)求直线AB的方程。
上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|FA|=2,|FB|=5,(1)求直线AB的方程。(2)在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求这个最大面积.
解:(1)由已知得
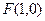 ,设点A坐标为
,设点A坐标为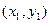 ,由
,由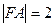 得
得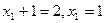
所以A(1,2),同理B(4,-4), 所以直线AB的方程为
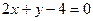 . (4分)
. (4分)(2)设在抛物线AOB这段曲线上任一点
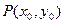 ,且
,且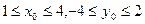 .
.则点P到直线AB的距离d=
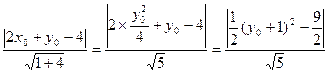
所以当
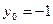 时,d取最大值
时,d取最大值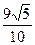 ,又
,又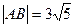
所以△PAB的面积最大值为
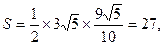 此时P点坐标为
此时P点坐标为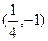 .
.法二:
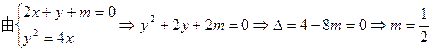
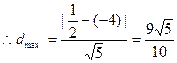 ,所以△PAB的面积最大值为
,所以△PAB的面积最大值为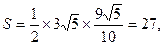
此时P点坐标为
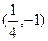
略

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
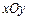 中的抛物线
中的抛物线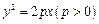 的焦点
的焦点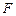 作一条倾斜角为
作一条倾斜角为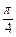 的直线与抛物线相交于A、B两点.
的直线与抛物线相交于A、B两点.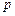 表示A、B之间的距离;
表示A、B之间的距离;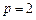 时,求
时,求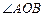 的余弦值.
的余弦值.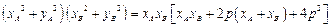 .
.
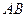 ⊥
⊥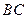 ,
,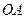 ∥
∥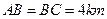 ,
,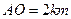 ,
, 曲线段
曲线段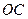 是以点
是以点 为顶
为顶 点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落
点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落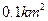 ).
).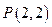 为
为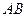 的中点,则抛物线C的方程为
的中点,则抛物线C的方程为 
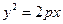 上,横坐标为4的点到焦点的距离为5,则
上,横坐标为4的点到焦点的距离为5,则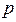 的值为( )
的值为( )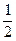 B 1 C 2 D 4
B 1 C 2 D 4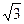 ,则M到该抛物线焦点的距离为
,则M到该抛物线焦点的距离为 的焦点为
的焦点为 ,准线与
,准线与 轴的交点为
轴的交点为 ,
, 为抛物线上的一点,且
为抛物线上的一点,且 ,则
,则 ( )
( )



