题目内容
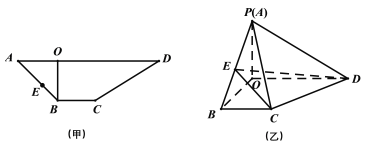
【题目】如图，在四棱锥
中，底面
是正方形，侧面
底面，且
，设
，
，
分别为
，
，
的中点.
（1）求证:平面
平面
;
（2）求直线
与平面
所成角的正弦值.
【答案】（1）证明见解析（2）
【解析】
（1）由
，得到
平面
，由
，得到
平面，从而得到平面
平面；（2）
为坐标原点，
，
，
分别为
，
，
轴建立空间直角坐标系，设
，表示出所需的点的坐标，然后得到平面
的法向量
，利用公式得到与
的夹角余弦值，从而得到答案.
解:（1）证明:
，
，
为
，
，的中点，
∴，
因为
平面，
平面
所以平面，
因为
是正方形，所以
，
所以
因为
平面，
平面，
所以平面
又
，且
，
平面
所以平面平面.
（2）
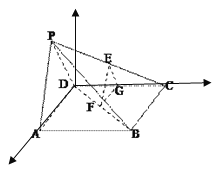
解:
平面
平面，过作面的垂线，
以为坐标原点，，，分别为，，轴建立空间直角坐标系.
设，则
，
，∴
又因为
，
所以
，
，
设平面的法向量
，
则
，则可取
，
，
所以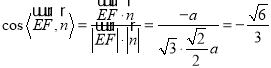
，
所以直线
与平面所成的角的正弦值为
.
练习册系列答案
相关题目
【题目】随着手机的普及，大学生迷恋手机的现象非常严重.为了调查双休日大学生使用手机的时间，某机构采用不记名方式随机调查了使用手机时间不超过
小时的
名大学生，将人使用手机的时间分成
组：
，
，
，
，
分别加以统计，得到下表，根据数据完成下列问题：
使用时间/时 |
|
|
|
|
|
大学生/人 |
|
|
|
|
|
（1）完成频率分布直方图；
（2）根据频率分布直方图估计大学生使用手机的平均时间.
【题目】南京市自
年成功创建“国家卫生城市”以来，已经连续三次通过“国家卫生城市”复审，
年下半年，南京将迎来第四次复审.为了了解市民绿色出行的意识，现从某单位随机抽取
名职工，统计了他们一周内路边停车的时间
（单位：
），整理得到数据分组及频率分布直方图如下：
组号 | 分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
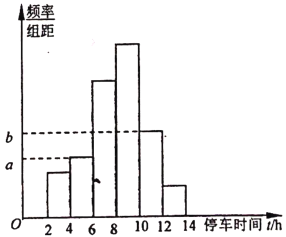
（1）从该单位随机选取一名职工，试估计其在该周内路边停车的时间少于
小时的概率；
（2）求频率分布直方图中
，
的值.