ƒøƒ⁄»ð
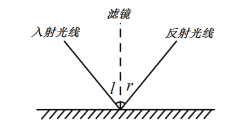
°æƒø°ø‘ƒ∂¡œ¬¡–”–πÿπ‚œþµƒ»Î…‰”Î∑¥…‰µƒ¡Ω∏ˆ ¬ µœ÷œÛ£∫œ÷œÛ£®1£©£∫π‚œþæ≠∆Ω√Êæµ∑¥…‰¬˙◊„»Î…‰Ω«”Î∑¥…‰Ω«œýµ»£®»ÁÕº£©£ªœ÷œÛ£®2£©£ªπ‚œþ¥”Õ÷‘≤µƒ“ª∏ˆΩπµ„≥ˆ∑¢æ≠Õ÷‘≤∑¥…‰∫ÛÕ®π˝¡Ì“ª∏ˆΩ𵄣®»ÁÕº£©£Æ ‘Ω·∫œ£¨…œ ˆ ¬ µœ÷œÛÕÍ≥…œ¬¡–Œ £∫
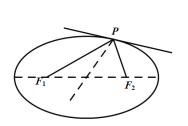
£®¢Ò£©”–“ªÕ÷‘≤–Õî«Ú◊¿£¨≥§÷·≥§Œ™2a£¨∂Ã÷·≥§Œ™2b£ÆΩ´“ª∑≈÷√”⁄Ω𵄥¶µƒ◊¿«Úª˜≥ˆ£Ææ≠π˝«Ú◊¿±þ‘µµƒ∑¥…‰£®ºŸ…Ë«Úµƒ∑¥…‰≥‰»´∑˚∫œœ÷œÛ£®2£©£©£¨∫Ûµ⁄“ª¥Œ∑µªÿµΩ∏√Ω𵄠±À˘æ≠π˝µƒ¬∑≥ú«Œ™S£¨«ÛSµƒ÷µ£®”√a£¨b±Ì 棩£ª
£®¢Ú£©Ω·¬€£∫Õ÷‘≤![]() …œ»Œµ„P£®x0£¨y0£©¥¶µƒ«–œþµƒ∑Ω≥ÃŒ™
…œ»Œµ„P£®x0£¨y0£©¥¶µƒ«–œþµƒ∑Ω≥ÃŒ™![]() £Æº«Õ÷‘≤Cµƒ∑Ω≥ÃŒ™C£∫
£Æº«Õ÷‘≤Cµƒ∑Ω≥ÃŒ™C£∫![]() £¨‘⁄÷±œþx£Ω4…œ»Œ“ªµ„MœÚÕ÷‘≤C“˝«–œþ£¨«–µ„∑÷±Œ™A£¨B£Æ«Û÷§£∫÷±œþlAB∫„π˝∂®µ„£∫
£¨‘⁄÷±œþx£Ω4…œ»Œ“ªµ„MœÚÕ÷‘≤C“˝«–œþ£¨«–µ„∑÷±Œ™A£¨B£Æ«Û÷§£∫÷±œþlAB∫„π˝∂®µ„£∫
£®¢Û£©π˝µ„T£®1£¨0£©µƒ÷±œþl£®÷±œþl–±¬ ≤ªŒ™0£©”ÎÕ÷‘≤C£∫![]() Ωª”⁄P°¢Q¡Ωµ„£¨ «∑ҥʑ⁄∂®µ„S£®s£¨0£©£¨ πµ√÷±œþSP”ÎSQ–±¬ ÷ƪ˝Œ™∂®÷µ£¨»Ù¥Ê‘⁄«Û≥ˆS◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
Ωª”⁄P°¢Q¡Ωµ„£¨ «∑ҥʑ⁄∂®µ„S£®s£¨0£©£¨ πµ√÷±œþSP”ÎSQ–±¬ ÷ƪ˝Œ™∂®÷µ£¨»Ù¥Ê‘⁄«Û≥ˆS◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®¢Ò£©S£Ω2£®a![]() £©£¨S£Ω2£®a
£©£¨S£Ω2£®a![]() £©£¨S£Ω4a£ª£®¢Ú£©÷§√˜º˚Ω‚Œˆ°°£®¢Û£©¥Ê‘⁄£¨∂®µ„S£®°¿3£¨0£©
£©£¨S£Ω4a£ª£®¢Ú£©÷§√˜º˚Ω‚Œˆ°°£®¢Û£©¥Ê‘⁄£¨∂®µ„S£®°¿3£¨0£©
°æΩ‚Œˆ°ø
£®¢Ò£©∏˘æð“‚∑÷◊¿«Úµ⁄“ª¥Œ”ΫÚ◊¿µƒ±þ‘µµƒΩ”¥•µ„Œ™≥§÷·µƒ¡Ω∏ˆ∂Àµ„ªÚ’‚¡Ω∏ˆ∂Àµ„Õ‚µƒ»Œ“ªµ„»˝÷÷«ÈøˆΩ¯––Ã÷¬€º¥ø….
£®¢Ú£©…ËM£®4,t£©,A£®x1,y1£©,B£®x2,y2£©,‘Ÿ∏˘æðÕ÷‘≤‘⁄µ„P£®x0,y0£©¥¶µƒ«–œþµƒ∑Ω≥ÃŒ™![]() º¥ø…«Ûµ√¡ΩÃı«–œþ∑Ω≥õƒ±Ì¥Ô Ω,‘Ÿ∏˘æðM£®4,t£©‘⁄¡ΩÃı«–œþ…œº¥ø…«Ûµ√lAB
º¥ø…«Ûµ√¡ΩÃı«–œþ∑Ω≥õƒ±Ì¥Ô Ω,‘Ÿ∏˘æðM£®4,t£©‘⁄¡ΩÃı«–œþ…œº¥ø…«Ûµ√lAB
µƒ÷±œþ∑Ω≥Ã.
£®¢Û£©…Ëlµƒ∑Ω≥ÃŒ™£∫x£Ωmy+1,‘Ÿ¡™¡¢÷±œþ”ÎÕ÷‘≤µƒ∑Ω≥Ã,«Ûµ√÷±œþSP”ÎSQ–±¬ ÷ƪ˝µƒ±Ì¥Ô Ω,‘Ÿ∏˘æð±Ì¥Ô Ω«ÛS£®s,0£©º¥ø….
£®¢Ò£©º«c![]() ,“ÚŒ™◊¿«Úµ⁄“ª¥Œ”ΫÚ◊¿µƒ±þ‘µµƒΩ”¥•µ„ø…ƒÐ «≥§÷·µƒ¡Ω∏ˆ∂Àµ„º∞’‚¡Ω∏ˆ∂Àµ„Õ‚µƒ»Œ“ªµ„»˝÷÷«Èøˆ,
,“ÚŒ™◊¿«Úµ⁄“ª¥Œ”ΫÚ◊¿µƒ±þ‘µµƒΩ”¥•µ„ø…ƒÐ «≥§÷·µƒ¡Ω∏ˆ∂Àµ„º∞’‚¡Ω∏ˆ∂Àµ„Õ‚µƒ»Œ“ªµ„»˝÷÷«Èøˆ,
À˘“‘,S£Ω2£®a©Åc£©ªÚS£Ω2£®a+c£©ªÚS£Ω4a£ª
º¥S£Ω2£®a![]() £©,S£Ω2£®a
£©,S£Ω2£®a![]() £©,S£Ω4a£ª
£©,S£Ω4a£ª
£®¢Ú£©…ËM£®4,t£©,A£®x1,y1£©,B£®x2,y2£©,‘Ú÷±œþlMA£∫![]() 1,lMB£∫
1,lMB£∫![]() 1,¥˙»ÎM÷–,µ√lMA£∫
1,¥˙»ÎM÷–,µ√lMA£∫![]() ty1£Ω1,lMB£∫
ty1£Ω1,lMB£∫![]() 2£Ω1,
2£Ω1,
‘Úµ„A,Bµƒ◊¯±Í¬˙◊„∑Ω≥ã∫![]() ty©Å1£Ω0,
ty©Å1£Ω0,
∫„π˝∂®µ„G£®![]() ,0£©£ª
,0£©£ª
£®¢Û£©”…“—÷™÷±œþπ˝µ„T£®1,0£©,…Ëlµƒ∑Ω≥ÃŒ™£∫x£Ωmy+1,P£®x,y£©,Q£®x',y'£©,¡™¡¢”ÎÕ÷‘≤µƒ∑Ω≥Ã’˚¿Ìµ√£∫£®9+m2£©y2+2my©Å8£Ω0,°ýy+y'![]() ,yy'
,yy'![]() ,
,
kSP![]() ,Õ¨¿Ìµ√kSQ
,Õ¨¿Ìµ√kSQ![]() ,°ýkSPkSQ
,°ýkSPkSQ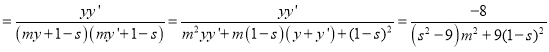 ,µ±s£Ω3 ±,kSPkSQ
,µ±s£Ω3 ±,kSPkSQ![]() ,
,
µ±s£Ω©Å3 ±,kSPkSQ![]() ,À˘“‘¥Ê‘⁄∂®µ„S£®°¿3,0£©, πµ√÷±œþSP”ÎSQ–±¬ ÷ƪ˝Œ™∂®÷µ£Æ
,À˘“‘¥Ê‘⁄∂®µ„S£®°¿3,0£©, πµ√÷±œþSP”ÎSQ–±¬ ÷ƪ˝Œ™∂®÷µ£Æ

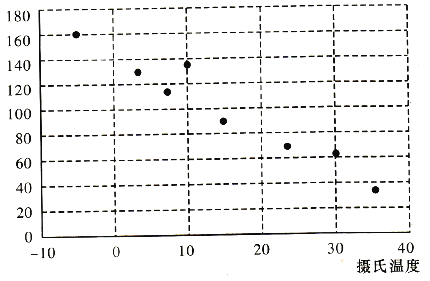
°æƒø°ø”–“ª∏ˆÕ¨—ߺ“ø™¡À“ª∏ˆ–°¬Ù≤ø£¨À˚Œ™¡À—–æø∆¯Œ¬∂‘»»“˚“˚¡œœ˙ €µƒ”∞œÏ£¨æ≠π˝Õ≥º∆£¨µ√µΩ“ª∏ˆ¬Ù≥ˆµƒ»»“˚±≠ ˝”ε±ÃÏ∆¯Œ¬µƒ…¢µ„Õº∫Õ∂‘±»±Ì£∫
…„ œŒ¬∂» |
|
|
|
|
|
|
|
|
»»“˚±≠ ˝ |
|
|
|
|
|
|
|
|
£®1£©¥”…¢µ„Õºø…“‘∑¢œ÷£¨∏˜µ„…¢≤º‘⁄¥”◊Û…œΩ«µΩ”“œ¬Ω«µƒ«¯”Ú¿Ô°£“Ú¥À£¨∆¯Œ¬”ε±ÃÏ»»“˚œ˙ €±≠ ˝÷ƺ‰≥…∏∫œýπÿ£¨º¥∆¯Œ¬‘Ω∏þ£¨µ±ÃϬÙ≥ˆ»•µƒ»»“˚±≠ ˝‘Ω…Ÿ°£Õ≥º∆÷–≥£”√œýπÿœµ ˝![]() ¿¥∫‚¡ø¡Ω∏ˆ±‰¡ø÷ƺ‰œþ–‘πÿœµµƒ«ø»ı.Õ≥º∆—ß»œŒ™£¨∂‘”⁄±‰¡ø
¿¥∫‚¡ø¡Ω∏ˆ±‰¡ø÷ƺ‰œþ–‘πÿœµµƒ«ø»ı.Õ≥º∆—ß»œŒ™£¨∂‘”⁄±‰¡ø![]() °¢
°¢![]() £¨»Áπ˚
£¨»Áπ˚![]() £¨ƒ«√¥∏∫œýπÿ∫Ыø£ª»Áπ˚
£¨ƒ«√¥∏∫œýπÿ∫Ыø£ª»Áπ˚![]() £¨ƒ«√¥’˝œýπÿ∫Ыø£ª»Áπ˚
£¨ƒ«√¥’˝œýπÿ∫Ыø£ª»Áπ˚![]() £¨ƒ«√¥œýπÿ–‘“ª∞„£ª»Áπ˚
£¨ƒ«√¥œýπÿ–‘“ª∞„£ª»Áπ˚![]() £¨ƒ«√¥œýπÿ–‘Ωœ»ı°£«Î∏˘æð“—÷™ ˝æð£¨≈–∂œ∆¯Œ¬”ε±ÃÏ»»“˚œ˙ €±≠ ˝œýπÿ–‘µƒ«ø»ı.
£¨ƒ«√¥œýπÿ–‘Ωœ»ı°£«Î∏˘æð“—÷™ ˝æð£¨≈–∂œ∆¯Œ¬”ε±ÃÏ»»“˚œ˙ €±≠ ˝œýπÿ–‘µƒ«ø»ı.
£®2£©£®i£©«Î∏˘æð“—÷™ ˝æð«Û≥ˆ∆¯Œ¬”ε±ÃÏ»»“˚œ˙ €±≠ ˝µƒœþ–‘ªÿπÈ∑Ω≥ãª
£®ii£©º«![]() Œ™≤ª≥¨π˝
Œ™≤ª≥¨π˝![]() µƒ◊Ó¥Û’˚ ˝£¨»Á
µƒ◊Ó¥Û’˚ ˝£¨»Á![]() £¨
£¨![]() .∂‘”⁄£®i£©÷–«Û≥ˆµƒœþ–‘ªÿπÈ∑Ω≥Ã
.∂‘”⁄£®i£©÷–«Û≥ˆµƒœþ–‘ªÿπÈ∑Ω≥Ã![]() £¨Ω´
£¨Ω´![]() ”Œ™∆¯Œ¬”ε±ÃÏ»»“˚œ˙ €±≠ ˝µƒ∫Ø ˝πÿœµ.“—÷™∆¯Œ¬
”Œ™∆¯Œ¬”ε±ÃÏ»»“˚œ˙ €±≠ ˝µƒ∫Ø ˝πÿœµ.“—÷™∆¯Œ¬![]() ”ε±ÃÏ»»“˚√ø±≠µƒœ˙ €¿˚»Û
”ε±ÃÏ»»“˚√ø±≠µƒœ˙ €¿˚»Û![]() µƒπÿœµ «
µƒπÿœµ «![]()
![]() £®µ•Œª£∫‘™£©£¨«ÎŒ µ±∆¯Œ¬
£®µ•Œª£∫‘™£©£¨«ÎŒ µ±∆¯Œ¬![]() Œ™∂ý…Ÿ ±£¨µ±Ãϵƒ»»“˚œ˙ €¿˚»Û◊Ð∂Ó◊Ó¥Û£ø
Œ™∂ý…Ÿ ±£¨µ±Ãϵƒ»»“˚œ˙ €¿˚»Û◊Ð∂Ó◊Ó¥Û£ø
£®≤Œøºπ´ Ω£©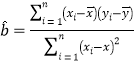 £¨
£¨![]() £¨
£¨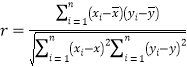
£®≤Œøº ˝æð£©![]() £¨
£¨![]() £¨
£¨![]()
![]() .
.
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() .
.
°æƒø°øπ˙º“ª∑æ≥±Í◊º÷∆∂®µƒø’∆¯÷ ¡ø÷∏ ˝”Îø’∆¯÷ ¡øµ»º∂∂‘”¶πÿœµ»Á±Ì£∫
ø’∆¯÷ ¡ø÷∏ ˝ | 0°´50 | 51°´100 | 101°´150 | 151°´200 | 201°´300 | 300“‘…œ |
ø’∆¯÷ ¡øµ»º∂ | 1º∂”≈ | 2º∂¡º | 3º∂«· ∂»Œ€»æ | 4º∂÷–∂»Œ€»æ | 5º∂÷ÿ ∂»Œ€»æ | 6º∂—œ÷ÿŒ€»æ |
”…»´π˙÷ÿµ„≥« –ª∑æ≥ºý≤‚Õ¯ªÒµ√10‘¬∑ðƒ≥ŒÂÃϺ◊≥« –∫Õ““≥« –µƒø’∆¯÷ ¡ø÷∏ ˝ ˝æð”√æ•“∂Õº±Ì æ»ÁÕº£∫
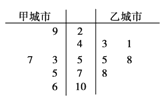
£®1£© ‘∏˘æð…œ√ʵƒÕ≥º∆ ˝æ𣨺∆À„º◊°¢““¡Ω∏ˆ≥« –µƒø’∆¯÷ ¡ø÷∏ ˝µƒ∑Ω≤Ó£ª
£®2£© ‘∏˘æð…œ√ʵƒÕ≥º∆ ˝æð£¨π¿º∆º◊≥« –ƒ≥“ªÃÏø’∆¯÷ ¡øµ»º∂Œ™2º∂¡ºµƒ∏≈¬ £ª
£®3£©∑÷±¥”º◊≥« –∫Õ““≥« –µƒÕ≥º∆ ˝æð÷–»Œ»°“ª∏ˆ£¨ ‘«Û¡Ω∏ˆ≥« –ø’∆¯÷ ¡øµ»º∂œýÕ¨µƒ∏≈¬ £Æπ©≤Œøº ˝æð£∫292+532+572+752+1062=23760£¨432+412+552+582+782=16003