题目内容
11.若α,β∈(π,$\frac{3}{2}$π),且tan2α>tan2β,则( )| A. | α<β | B. | α>β | C. | α+β>3π | D. | α+β<2π |
分析 由已知α,β∈(π,$\frac{3}{2}$π),得到tanα>tanβ>0,结合三角函数的单调性可得α,β的大小.
解答 解:因为α,β∈(π,$\frac{3}{2}$π),所以tanα>0,tanβ>0,
又tan2α>tan2β,所以tanα>tanβ>0,
函数y=tanx在∈(π,$\frac{3}{2}$π)是增函数,所以α>β;
故选:B
点评 本题考查了由正切函数的单调性,判断角度的大小;关键是明确正切函数在∈(π,$\frac{3}{2}$π),的单调性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.曲线y=lnx在点x=2处的切线的斜率为( )
| A. | ln2 | B. | 2 | C. | $\frac{1}{2}$ | D. | 0 |
6.已知某几何体的三视图如图所示,则该几何体的体积为( )
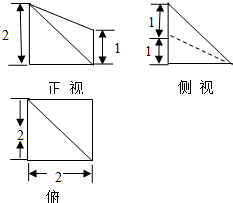

| A. | 3 | B. | $\frac{10}{3}$ | C. | $\frac{11}{3}$ | D. | $\frac{8}{3}$ |