题目内容
数列{an}的前n项和为Sn,a1=1,an+1=2Sn(n∈N*),则an=______.
当n≥1时,an+1=2Sn,an+2=2Sn+1,
所以两式相减得,an+2-an+1=2Sn+1-2Sn=2an+1,
所以an+2=3an+1,所以从第3项起数列{an}是以a2为首项,以3为公比的等比数列,所以a2=2S1=2,
所以an=2?3n-2,n≥2,因为a1=1不满足an,
所以an=
.
故答案为:an=
.
所以两式相减得,an+2-an+1=2Sn+1-2Sn=2an+1,
所以an+2=3an+1,所以从第3项起数列{an}是以a2为首项,以3为公比的等比数列,所以a2=2S1=2,
所以an=2?3n-2,n≥2,因为a1=1不满足an,
所以an=
|
故答案为:an=
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
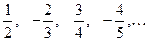 的一个通项公式是 。
的一个通项公式是 。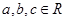 ,且
,且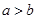 ,则 ( )
,则 ( )



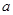 、
、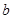 为非零实数,
为非零实数,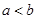 ,则下列不等式成立的是( )
,则下列不等式成立的是( )


