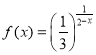��Ŀ����
����Ŀ��һ�����С��Ϸ�Ĺ������£�ÿ����Ϸ����������Σ�ÿ�λ���Ҫô����һ�����֣�Ҫô���������֣�ÿ����Ϸ�������κ���һ�����ֻ��10�֣������������ֻ��20�֣������������ֻ��100�֣�û�г���������۳�200�֣�����ã�200�֣�����ÿ�λ��ij������ֵĸ���Ϊ![]() ���Ҹ��λ����Ƿ���������������
���Ҹ��λ����Ƿ���������������
��1����������Ϸ��������һ�ֳ������ֵĸ����Ƕ��٣�
��2����ÿ����Ϸ��õķ���ΪX����X�ķֲ��м���ѧ������
���𰸡���1��![]() ��(2)������
��(2)������
��������
��1�����ö����¼����ó�P��A1����P��A2����P��A3����P��X����200��![]() �����P��A1A2A3�����ɵó�1��P��A1A2A3����
�����P��A1A2A3�����ɵó�1��P��A1A2A3����
��2��X���ܵ�ȡֵΪ10��20��100����200�����ü��θ��ʹ�ʽ�ó������Ӧ�ĸ��ʣ��ó��ֲ��У�
��1���衰��i����Ϸû�г������֡�Ϊ�¼�Ai��i��1��2��3������
P��A1����P��A2����P��A3����P��X����200��![]() ��
��
���ԡ�������Ϸ��������һ�ֳ������֡��ĸ���Ϊ1��P��A1A2A3����1��![]() ��
��
��ˣ���������Ϸ������һ�ֳ������ֵĸ�����![]() ��
��
��2��X���ܵ�ȡֵΪ10��20��100����200���������⣬��
P��X��10��![]() ��
��![]() ��1����1
��1����1![]() ��2
��2![]() ��
��
P��X��20��![]() ��
��![]() ��2����1
��2����1![]() ��1
��1![]() ��
��
P��X��100��![]() ��
��![]() ��3����1
��3����1![]() ��0
��0![]() ��
��
P��X����200��![]() ��
��![]() ��0����1
��0����1![]() ��3
��3![]() ��
��
��X�ķֲ���Ϊ��
X | 10 | 20 | 100 | ��200 |
P |
|
|
|
|
E(��)��![]() .
.