题目内容
若ABC的三边长分别为a, b, c，其内切圆半径为r，则S△ABC=(a+b+c）·r，
类比这一结论到空间，写出三棱锥中的一个正确结论为
类比这一结论到空间，写出三棱锥中的一个正确结论为
若四棱锥A-BCD的四个面的面积分别为
，其内切球半径为R，
则
，其内切球半径为R，则
若三棱锥A-BCD的四个面的面积分别为，其内切球半径为R，球心为O，连接OA、OB、OC、OD则三棱锥被分成四个小三棱锥，分别为O-ACD、O-ABC、O-ABD、O-BCD由内切球知四个小三棱锥的高都是R，
所以
，其内切球半径为R，球心为O，连接OA、OB、OC、OD则三棱锥被分成四个小三棱锥，分别为O-ACD、O-ABC、O-ABD、O-BCD由内切球知四个小三棱锥的高都是R，所以
练习册系列答案
相关题目
（
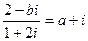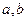
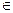R），其中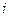
为虚数单位，则
( )
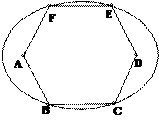
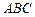中，
，求证
.
，
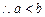，画线部分是演绎推理的是（） 
时
（用含
的式子表示）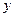
＝
＋
（
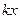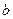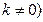在Ｒ上是增函数，而
＋
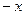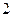是一次函数，所以
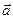的性质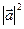
=
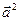类比得到复数
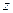的性质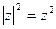
；