题目内容
11.已知实数x,y满足$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$,则(x-2)2+y2的最小值为$\frac{1}{2}$.分析 由约束条件作出可行域,(x-2)2+y2的几何意义为可行域内动点(x,y)与定点P(2,0)距离的平方,然后结合点到直线的距离公式得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$作出可行域如图,
(x-2)2+y2的几何意义为可行域内动点(x,y)与定点P(2,0)距离的平方.
由图可知,P(2,0)与可行域内动点距离的最小值为d=$\frac{|1×2-1|}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
∴(x-2)2+y2的最小值等于${d}^{2}=(\frac{\sqrt{2}}{2})^{2}=\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
6.已知A,B,C为△ABC的三个内角,命题p:A=B;命题q:sinA=sinB.则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
3.已知等差数列{an}满足:a3=13,a13=33,则数列{an}的公差为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.如图是一个几何体的三视图,其俯视图的面积为8$\sqrt{2}$,则该几何体的表面积为( )


| A. | 8 | B. | 20+8$\sqrt{2}$ | C. | 16 | D. | 24+8$\sqrt{2}$ |
 对某电子元件进行寿命追踪调查,所得情况如频率分布直方图.(1)图中纵坐标y0处刻度不清,根据图表所提供的数据还原y0;
对某电子元件进行寿命追踪调查,所得情况如频率分布直方图.(1)图中纵坐标y0处刻度不清,根据图表所提供的数据还原y0;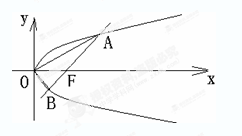 过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.
过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点. 有5位工人在某天生产同一零件,所生产零件个数的茎叶图如图所示,已知它们生产零件的平均数为10,标准差为$\sqrt{2}$,则|x-y|的值为( )
有5位工人在某天生产同一零件,所生产零件个数的茎叶图如图所示,已知它们生产零件的平均数为10,标准差为$\sqrt{2}$,则|x-y|的值为( )