题目内容
【理科生做】已知点A、B的坐标分别是(0,-1),(0,1),直线AM、BM相交于点M,且它们的斜率之积为-1.
(1)求点M轨迹C的方程;
(2)若过点(2,0)且斜率为k的直线l与(1)中的轨迹C交于不同的两点E、F(E在D、F之间),记△ODE与△ODF面积之比为λ,求关于λ和k的关系式,并求出λ取值范围(O为坐标原点).
(1)求点M轨迹C的方程;
(2)若过点(2,0)且斜率为k的直线l与(1)中的轨迹C交于不同的两点E、F(E在D、F之间),记△ODE与△ODF面积之比为λ,求关于λ和k的关系式,并求出λ取值范围(O为坐标原点).
分析:(1)设M(x,y),由题意可得kAM•kBM=-1,利用斜率计算公式可得
•
=-1(x≠0),化简即可;
(2)如图所示,设E(x1,y1),F(x2,y2),(x1>0>x2).则
=
=λ=
.(*)
直线l的方程为y=k(x-2)(0<y≤1)与圆的方程联立可得△>0,再利用求根公式可得x1,x2,代入(*)即可.
| y+1 |
| x |
| y-1 |
| x |
(2)如图所示,设E(x1,y1),F(x2,y2),(x1>0>x2).则
| S△ODE |
| S△ODF |
| |DE| |
| |DF| |
| 2-x1 |
| 2-x2 |
直线l的方程为y=k(x-2)(0<y≤1)与圆的方程联立可得△>0,再利用求根公式可得x1,x2,代入(*)即可.
解答:解:(1)设M(x,y),由题意可得kAM•kBM=-1,∴
•
=-1(x≠0),化为x2+y2=1(x≠0).
∴点M轨迹C的方程为x2+y2=1(x≠0);
(2)如图所示,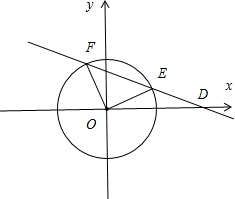 设E(x1,y1),F(x2,y2),(x1>0>x2).
设E(x1,y1),F(x2,y2),(x1>0>x2).
则
=
=λ.
直线l的方程为y=k(x-2).
联立
,(0<y≤1),化为(1+k2)x2-4k2x+4k2-1=0,
由△=16k4-4(1+k2)(4k2-1)>0,及1≥y>0,解得-
<k<0.
∴x=
,取x1=
,x2=
.
∴λ=
=
.由-
<k<0.
可得
<λ<1.
| y+1 |
| x |
| y-1 |
| x |
∴点M轨迹C的方程为x2+y2=1(x≠0);
(2)如图所示,
 设E(x1,y1),F(x2,y2),(x1>0>x2).
设E(x1,y1),F(x2,y2),(x1>0>x2).则
| S△ODE |
| S△ODF |
| |DE| |
| |DF| |
直线l的方程为y=k(x-2).
联立
|
由△=16k4-4(1+k2)(4k2-1)>0,及1≥y>0,解得-
| ||
| 3 |
∴x=
4k2±2
| ||
| 2(1+k2) |
2k2+
| ||
| 1+k2 |
2k2-
| ||
| 1+k2 |
∴λ=
| 2-x1 |
| 2-x2 |
2-
| ||
2+
|
| ||
| 3 |
可得
| 1 |
| 3 |
点评:熟练掌握圆的标准方程、斜率计算公式、直线与圆相交问题转化为方程联立得到△>0及利用求根公式得到实数根、函数的单调性等是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目