题目内容
(2012•大连模拟)已知A、B、C是△ABC的三个内角,且满足2sinB=sinA+sinC,设B的最大值为B0.
(Ⅰ)求B0的大小;
(Ⅱ)当B=
时,求cosA-cosC的值.
(Ⅰ)求B0的大小;
(Ⅱ)当B=
| 3B0 | 4 |
分析:(Ⅰ)利用正弦定理化简已知的等式得到2b=a+c,表示出b,再利用余弦定理表示出cosB,将表示出的b代入,整理后,利用基本不等式可得出cosB的最小值,根据余弦函数在(0,π)上单调递减,利用特殊角的三角函数值即可求出B的最大值;
(Ⅱ)设所求的式子为x,记作①,由B与B0的关系及B0的度数,求出B的度数,代入已知的等式sinA+sinC=2sinB中,得到sinA+sinC的关系式,记作②,由①2+②2化简后,根据B的度数,求出A+C的度数,代入化简后的式子中,得到关于x的方程,求出方程的解得到x的值,即为所求式子的值.
(Ⅱ)设所求的式子为x,记作①,由B与B0的关系及B0的度数,求出B的度数,代入已知的等式sinA+sinC=2sinB中,得到sinA+sinC的关系式,记作②,由①2+②2化简后,根据B的度数,求出A+C的度数,代入化简后的式子中,得到关于x的方程,求出方程的解得到x的值,即为所求式子的值.
解答:解:(Ⅰ)由2sinB=sinA+sinC,利用正弦定理化简得:2b=a+c,即b=
,
由余弦定理知cosB=
=
(2分)
=
≥
=
,(4分)
∵y=cosx在(0,π)上单调递减,
则B的最大值为B0=
;(6分)
(Ⅱ)设cosA-cosC=x,①(8分)
∵B=
=
,
∴sinA+sinC=2sinB=
,②
由①2+②2得,2-2cos(A+C)=x2+2.(10分)
又A+C=π-B=
,
∴x=±
,即cosA-cosC=±
.(12分)
| a+c |
| 2 |
由余弦定理知cosB=
| a2+c2-b2 |
| 2ac |
a2+c2-(
| ||
| 2ac |
=
| 3(a2+c2)-2ac |
| 8ac |
| 3(2ac)-2ac |
| 8ac |
| 1 |
| 2 |
∵y=cosx在(0,π)上单调递减,
则B的最大值为B0=
| π |
| 3 |
(Ⅱ)设cosA-cosC=x,①(8分)
∵B=
| 3B0 |
| 4 |
| π |
| 4 |
∴sinA+sinC=2sinB=
| 2 |
由①2+②2得,2-2cos(A+C)=x2+2.(10分)
又A+C=π-B=
| 3π |
| 4 |
∴x=±
| 4 | 2 |
| 4 | 2 |
点评:此题考查了正弦、余弦定理,基本不等式,余弦函数的单调性,诱导公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
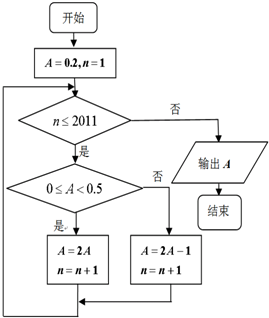 (2012•大连模拟)已知某程序框图如图所示,则该程序运行后,输出的结果为( )
(2012•大连模拟)已知某程序框图如图所示,则该程序运行后,输出的结果为( )