题目内容
（2012•大连模拟）在平行四边形ABCD中，∠BAD=60°，AD=2AB，若P是平面ABCD内一点，且满足x
+y
+
=
（x，y∈R），则当点P在以A为圆心，
|
|为半径的圆上时，实数x，y应满足关系式为（ ）
| AB |
| AD |
| PA |
| 0 |
| ||
| 3 |
| BD |
分析：设出AB，求出BD，利用已知条件以及余弦定理，求得对角线|
丨，根据向量加法和减法的三角形法则可得
=x
+y
，两边平方即可求得结果．
| BD |
| AP |
| AB |
| AD |
解答：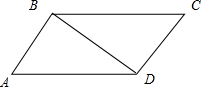
解：∵AD=2AB，设AB=1，则AD=2
∵在平行四边形ABCD中，∠BAD=60°，
∴DB=
，
∵x
+y
+
=
∴
=x
+y
，
|
|=
|
|=1，
∵点P在以A为圆心，1为半径的圆上，
∴
2=（x
+y
）2，
即1=x2
2+y2
2+2xy
•
=x2+4y2+2xy
故选D．
解：∵AD=2AB，设AB=1，则AD=2∵在平行四边形ABCD中，∠BAD=60°，
∴DB=
| 3 |
∵x
| AB |
| AD |
| PA |
| 0 |
∴
| AP |
| AB |
| AD |
|
| AP |
| ||
| 3 |
| BD |
∵点P在以A为圆心，1为半径的圆上，
∴
| AP |
| AB |
| AD |
即1=x2
| AB |
| AD |
| AB |
| AD |
故选D．
点评：本题考查余弦定理和向量的减法的三角形法则以及向量的数量积的定义，其中把已知条件化简为
=x
+y
，是解题的关键，属中档题．
| AP |
| AB |
| AD |
练习册系列答案
阅读快车系列答案
相关题目
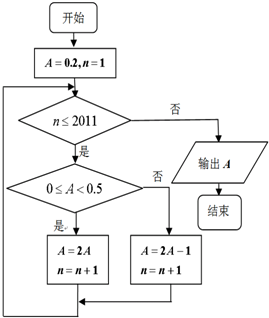（2012•大连模拟）已知某程序框图如图所示，则该程序运行后，输出的结果为（ ）